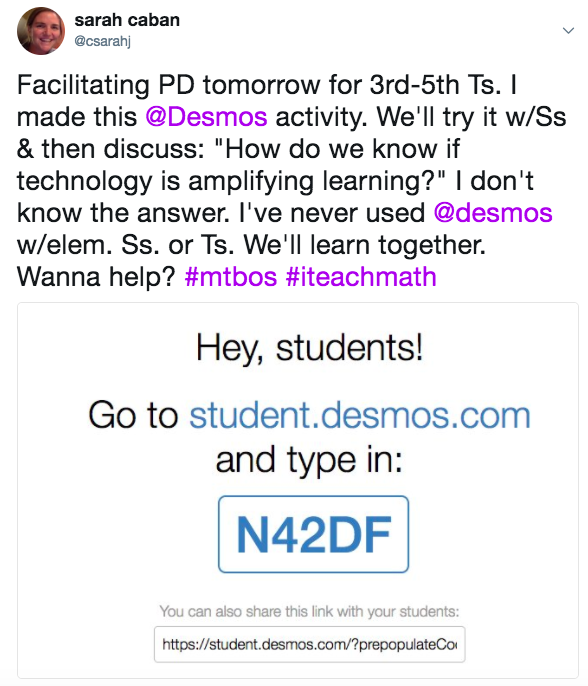
I haven’t been able to write much on my blog for the last two years because I have been busy writing the 5th grade course for the Illustrative Mathematics K-5 math curriculum. I am humbled and honored to share some of the story my colleagues and I are writing.
From the start of the year, we want students to know they are capable of engaging in grade level mathematics. In the Opportunity Myth (2018), data has shown there is an opportunity gap for historically marginalized students between the grade level expectations laid out in standards and students’ opportunities to engage with this content in their math classes. Oftentimes, grade level content is withheld from students because they are perceived as being not “ready” and, therefore, they are restricted to only engage in below grade level work. If we want to close the opportunity gap, we have to do many things differently than we have done in the past, one of which is re-examine the sequence of the content we put in front of students. The Illustrative Mathematics K-5 story of fifth grade was intentionally written so all students have access to grade level content.
Typically, many 5th grade math curricula start the year with units that focus on place value concepts and whole number multiplication and division algorithms. When considering whether to start the year this way, we wondered:
- What message does the mathematical content in the early units of the year send to students about what it means to ‘do math’ and what is valued in math class?
- What assumptions might educators make about students based on their successes or challenges with multiplication and division algorithms at the beginning of the year?
- How might these assumptions impact students’ access to grade level content throughout the course of the year?
Extend an Invitation
From the start of the year, we want to send the message that mathematics is an opportunity to be curious, collaborative, and playful. To do this, we begin by introducing students to the concept of volume. Being a new concept to fifth graders, it naturally invites students to be curious and creative, while at the same time offers teachers the opportunity to notice and build on what students do know and can do. It also diminishes, if not eliminates, the assumptions both teachers and students might make about what it looks like to be ‘good at math’.
Students begin their study of volume with many opportunities to build with unit cubes and use familiar words and phrases to explain the layered structure of rectangular prisms. Teachers listen for and display the words students use, such as “slices”, “groups”, or “layers”, to describe how they counted the cubes to determine the volume. Students connect their less formal language to multiplication expressions that represent the volume of rectangular prisms before they are introduced to more formal math vocabulary and procedures.
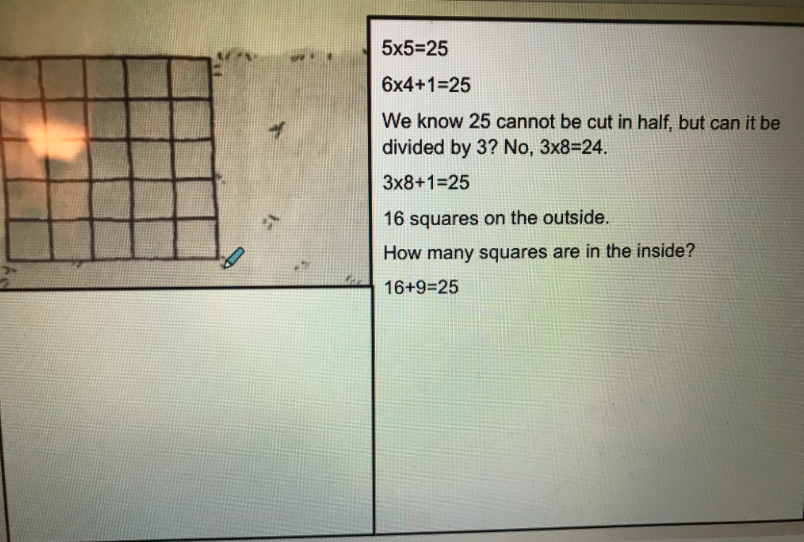
How do the expressions 5 x 24 and 6 x 20 represent the volume of the rectangular prism? Explain or show your reasoning.
Throughout unit 1, the measure of prism side lengths were chosen to encourage students to make sense of concepts of volume while they continue to strengthen their fluency with multiplication. Over time, students connect their informal strategies for finding the volume of rectangular prisms to generalized formulas. Later in the year, after learning the standard algorithm for multiplication in unit 4, students solve problems involving volume with larger multi-digit numbers as side length measures. This progression increases the opportunities for students to be successful with multiplication and division algorithms and decreases the likelihood that they will be perceived as not ready for new grade level topics because of their proficiency with computation. Therefore, we believe these choices will decrease the opportunity gap and increase student access to grade level content.
Put Fractions in the Forefront
Beyond Unit 1, we want to continue to maximize students’ opportunities to access grade level content. In Units 2 and 3, we introduce grade level content while providing ongoing opportunities to reinforce prior grade level understandings and fluencies, all within the work of fractions. While many curriculums organize whole number computation before fractions, this sequence has implications for extending an opportunity gap. If students are perceived as not being able to use whole number multiplication and division algorithms correctly, they may be confined to remediation cycles and denied the opportunity to engage with grade level fraction concepts and procedures. We know that understanding fraction operations is a major indicator of success with topics in high school mathematics so we want to ensure that each student has the opportunity to make sense of grade level fraction understandings and operations early in the year ( Siegler et. al., 2012, p.695).
Continue to Build on Prior Grade Level Content
In units 2 and 3, students revisit the meaning of fractions, multiplication, and division. They connect what they know about these topics to new learning.
Students begin unit 2 by interpreting a fraction as division of the numerator by the denominator. Through this work, they continually deepen their conceptual understanding of fractions and division. In the example below, students connect what they know about unit fractions and division.
- Complete the table.
| sandwiches | number of people sharing a sandwich | amount of sandwich for each person | division expression |
| 1 | 2 | ||
| 1 | 3 | ||
| 1 | 4 | ||
| 1 | 10 | ||
| 1 | 25 |
- Choose one row of the table and draw a diagram to show your reasoning for that row.
- What patterns do you notice?
As the unit progresses, students extend their understanding of multiplication as they multiply a whole number by a fraction. In the example below, students leverage what they know about whole number multiplication to solve problems involving multiplication of a whole number and a unit fraction.
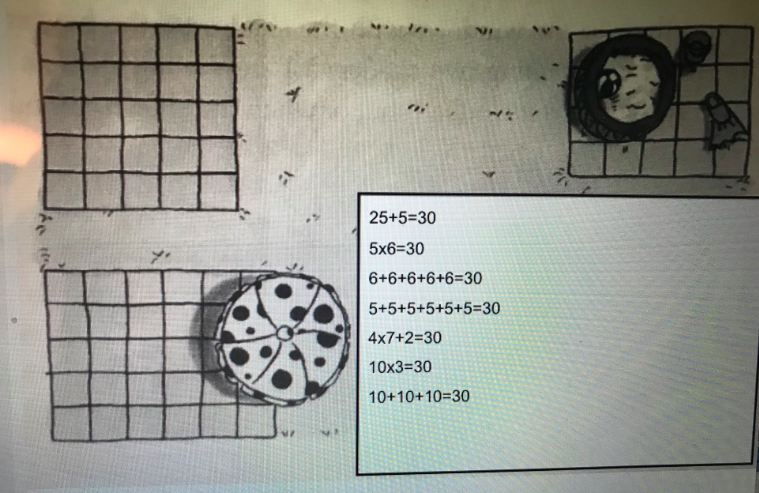
Find the area of the shaded region. Explain or show your reasoning.
In unit 3, students continue to use area diagrams to make sense of fraction multiplication. They build on the new understanding of multiplying a whole number by a fraction while applying prior grade understanding of area. They recognize, when multiplying fractions, the unit is the size of the piece being tiled within the unit square. They count those unit tiles by multiplying the number of tiles in each shaded row by the number of shaded rows.
For example when asked to determine the area of the shaded region below, students know that the unit square is partitioned into a array, so the size of each tile is . They then multiply to find how many tiles are shaded and determine that the area of the shaded region is. Students later apply these understandings to multiply any two fractions.
Students are offered another opportunity to revisit the major work of prior grades in the context of the major work of 5th grade when they are introduced to division of a unit fraction by a whole number and a whole number by a unit fraction. As shown in the example below, the sequence we chose offers students the opportunity to be curious and creative while deepening and extending their understanding of the meaning of division.
Sequencing fraction multiplication and division before whole number algorithms invites teachers to notice and celebrate what students do know about multiplication and division and minimizes the chances of teachers and students making assumptions about what students don’t know about fraction operations.
Make Algorithms Accessible
By the time students encounter whole number multiplication and division algorithms in unit 4, they have had significant experience building the necessary fluencies and understandings to be successful. Teachers have had significant opportunities to notice what each student knows and can do in regards to applying concepts of multiplication and division.
In telling the story of 5th grade, we chose to begin with an invitation to engage in grade level mathematics, introduce fractions early in the year, and postpone multi-digit multiplication and division algorithms until later in the year. We think these choices will:
- send the message that each student is creative, curious, and capable of doing grade level math in the beginning of the year.
- support teachers to notice and build on what students know and can do.
- increase opportunities for students to access grade level content.
We hope these choices lead to a world where more historically marginalized students have the opportunity to know, use, and enjoy mathematics.


































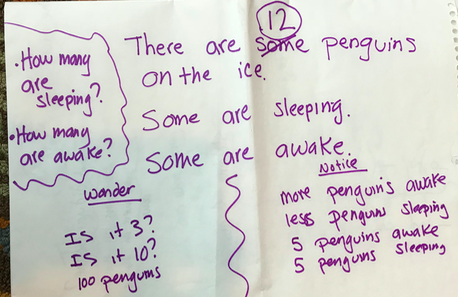
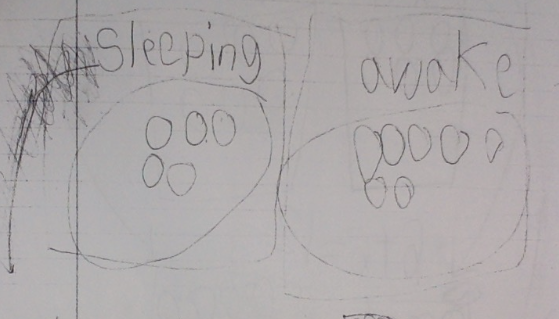
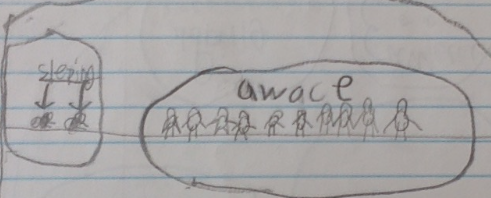
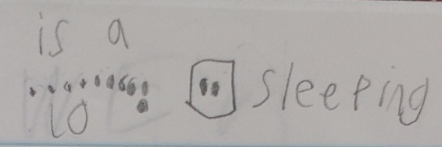

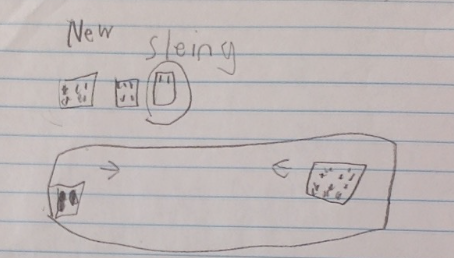








 Calvin can count forwards and backwards by tens, off the decade! He might not be able to do it all the time, but he can certainly do it. Now, we have to help him develop his place value understanding and connect it to what he knows about counting. I have been carefully observing Calvin during class lately. Here are some other things he can do:
Calvin can count forwards and backwards by tens, off the decade! He might not be able to do it all the time, but he can certainly do it. Now, we have to help him develop his place value understanding and connect it to what he knows about counting. I have been carefully observing Calvin during class lately. Here are some other things he can do:



 I opened Powerpoint and started messing around with arrays. The first few images I created only had 6 dots in them.
I opened Powerpoint and started messing around with arrays. The first few images I created only had 6 dots in them.