About two weeks ago, which is 100 years in Twitter time, I saw this tweet by Elizabeth Raskin:

I thought, “hmm. -4.8 plus seven jumps towards the positive side of things equals….-3.8, -2.8, -1.8, -.8, 1.8, 2.8. Yup. Makes sense to me.
So… why is this her favorite mistake? Hold on. Let me try that again:
-4.8 plus seven jumps towards the positive side of things equals….-3.8, -2.8, -1.8, -.8, 1.8, 2.8. Yup. Makes sense to me…..Wait. What?
Then, I did the same thing AGAIN. I won’t bore you with the details.
At this point I felt stuck and confused. I also felt curious and determined. Why is this her favorite mistake? What am I missing? I decided to try to solve the problem on my own, without looking at the student’s work. I wondered how many hops would it take to get back to zero? +4.8. Okay. How many hops do I still need to make to cover the total of 7 hops? 2.2. So….. the answer is 2.2 Oh!!!! I get it. This IS a cool mistake.
I responded to Elizabeth:
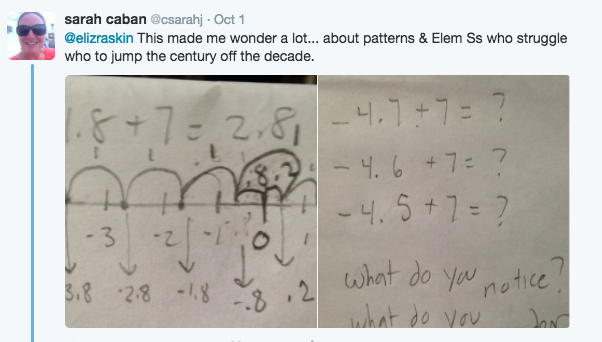
I wondered how I could use this problem with elementary teachers. This semester, two of our elementary schools are participating in learning rounds which focus on the NCTM teaching practice, Support Productive Struggle in Learning Math. In mixed grade level teams, we visit 2-3 classrooms and look for evidence of this practice. We record evidence of “look for’s” that we think we see:

Finally, during the debriefing, we try to synthesize our observations to increase our understanding of the practice.
To prepare us for each learning round, I facilitate a professional development session that takes place during a staff meeting prior to the observations. Elizabeth’s problem pushed my thinking about productive struggle. I decided to use it as my entry point to explore this teaching practice with the staff.
I knew I was going to be working with staff in two different buildings, but I decided to plan the same general session and adapt it to the needs of the staff. I thought I would learn a ton from the first session that would impact how I facilitated the second session (and I did). In the interest of blog efficiency, I have combined the experiences.
As the teachers settled into our staff meeting, I explained that our learning target would be to identify characteristics of productive struggle. I shared our guiding questions for this series of learning rounds:
- What is the difference between productive struggle and unproductive struggle?
- How do developmental stages and prior knowledge impact whether a struggle is productive?
I told the story about Elizabeth’s Tweet. I showed them a poster with the problem on it. The elementary teachers who have been in our district for at least three years are used to doing math together, but that doesn’t mean it is easy or comfortable for all of them to take math risks in front of their peers. Sadly, I knew that there would be at least a few teachers whose heart rates would increase as they experienced genuine panic about solving a math problem. Fortunately, our elementary schools are small. This building has seven k-5 teachers. They depend on each other for support. I encouraged them to work together if they wanted to. I told them it was okay to struggle. I shared that it took me several tries to figure it out. I asked them to try to solve the problem in several different ways so they could truly understand the student’s mistake.
The teachers dove right into the problem. One group (the kindergarten teacher and the second grade teacher) saw it right away. Here is their justification:

Some other teachers experienced similar disequilibrium to mine:
- “Can we change it to 7 – 4.8?”
- “Why am I getting 3.6?”
- “If I start at 5, do I have to add .2 or subtract .2 when I get to 2?”
Then I showed the teachers this problem:

I asked them to show multiple ways to arrive at the solution. Here is an example of the strategies they used (Incidentally, it is the work of the same two teachers whom I referenced in the first problem):

Then, I asked, “What is the same about these problems? What is different?”
“They both use a numberline, but one deals with crossing zero and one deals with crossing a decade.”
“They both have to do with place value patterns.”
Tell me more.
“Well, crossing a hundred is challenging because the patterns in the ten place change -now you have a hundreds place.”
Me: And what about the first problem?
“The pattern in the tenths place changes AND it is even more difficult because of the transition from negative to positive.”
Me: Can you see that on the number line?
“Yes!” (Points to change from -.8 to +.2)
“Both problems have to do with decomposing.”
“You can use compensation for both…. wait. Can you? How do you use compensation with negative numbers?”
“Well. If you add 1 jump of -.2 to -4.8, you will land on -5. So….Wait. Is that constant difference?”
“Keep going. If we add -.2 to the 7, we will get 6.8. Then we would have -5 + 6.8. That doesn’t work because the answer is 1.8.”
“What if you add +.2 to 7. Then, we would have -5 + 7.2. Yes!! That works. -5 +5 is 0 plus 2.2 is 2.2. But why do we have to make it positive?”
At this point, I was so excited about all the math that these K-5 teachers were doing. I was also stressed out because we had about 15 minutes left in our staff meeting and we had yet to identify characteristics of productive struggle. Should I just tell them all the rules for adding and subtracting positive and negative numbers? Give them a link to a Kahn Academy video? Maybe assign them 42 practice problems? I decided to go with being honest.
“You are doing some awesome thinking. It seems like you are engaged in productive struggle. I am too. I am also trying to figure out how the rules for adding and subtracting positive and negative numbers impact the discovery you just made. I need to explore it more and I encourage you too, as well. Maybe we can revisit the same problem next month and share what we learned. For now, I would love to hear what you think it looks like and sounds like when someone is engaged in struggle.”
“It looks like us trying to solve that negative number problem.”
So, what were we doing and saying that tells you we were engaged in struggle?
- making mistakes
- asking questions
- talking through our thinking
- saying bits and pieces of information that are leading up to a solution
- crossing things out
- trying once to see if your answer makes sense, deciding it doesn’t, and trying again
- saying, “wait. what?”
I asked if there was anything that they see in their classrooms that wasn’t on the list. They agreed that they see a lot of the same evidence of struggle in their classrooms. They added these:
- student sharing the wrong answer, but is totally convinced he is right
- students arguing
- “I don’t get it”
- students destroying his/her paper
This brought us back to one of our guiding questions, What is the difference between productive struggle and unproductive struggle? I asked the teachers to place some of their evidence on a continuum:

Then, I asked, “How do we keep the struggle productive?”
(Thoughtful silence as the clock ticked closer to 4:00.)
Slowly, they came up with some ideas:
- You have to have a culture where it is okay to disagree
- ..and mistakes are valued
- You have to anticipate who will know what and how you will navigate confusion
- You have to know when it is time to take a break or move on
- You have to ask the right questions
- It is hard. It is really hard… to balance pushing their thinking without giving them answers and/or confusing them to the point of frustration.
Me: Who is it hard for?
“The student… and, well, me.”
Me: Who struggles more?
“Good question. It depends.”
(More thoughtful silence and clock ticking.)
Me: “This is a huge question. I don’t think we can answer it in a day. We can come back to it each time we meet and discuss how our thinking is evolving. Thanks for taking a risk with me today. I can’t wait to be a part of your lessons tomorrow on learning rounds. I always learn so much from all of you.”
And learn I did, from each of the 11 classrooms that I got to observe. I wish I had time to write a blog about each and every one of them, especially my new hero, Mrs. Chalmers, who took a huge risk and offered her kindergarten students a 7 foot long piece of yarn on which to place the numbers 1-10. She navigated their struggle (and her own) with deliberate thought and humble presence. Thank you Mrs. Chalmers.

