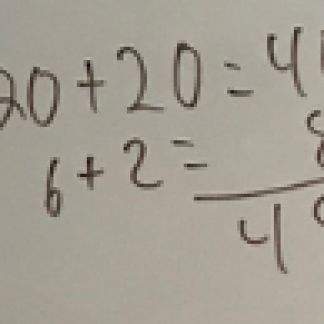Recently, during a Number Talk, I wrote this problem on the board and asked students to show me a quite thumb if the problem made sense. Then, I encouraged them to try to find a solution using some of the strategies we have been working on.

26 + 10 = ________

Calvin mumbled something under his breath. Students started raising their fingers to indicate how many strategies they had used. Calvin crossed his arms and started to kick the air as he slunk down into his chair. I asked the students to whisper the answer on the count of three. I heard a chorus of “36”. I wrote the next problem on the board.

26 + 12 = ________

Calvin glared at me. He growled. He turned his back to me. Mrs. X went over to him and he whispered to her as I continued the number talk.  When Mrs. X came back over to me, she whispered, “he’s mad at you because you won’t stack the numbers.” I nodded to her and continued on with the next problem.

26 + 22 = ________

Calvin glanced at me with angry eyes. Then, he looked at Mrs. X and snarled, “She’s not stacking it!” My quiet thumb dropped to my side. I took a breath, looked Calvin in the eyes, and responded, “Calvin, if you would like me to write the problem a different way, I can do that, but you need to use your words and ask me. I am happy to help you if you ask me to.” Then, I went back to thinking about 26+22. Calvin kicked the air and turned away from me. After some quiet think time, I collected solutions and asked for volunteers to defend them. Jason told us that he decomposed and added. I recorded his thinking as he spoke.

I said, “This strategy reminds me a little bit of the one Calvin likes to use.  We don’t have it listed on our strategies menu, but I think maybe we should. Calvin, did you want to talk about stacking?”

Calvin turned around. His shoulders settled. He asked, “can you write the numbers so they are stacked? That is the only way I can do it.”

“Of course I can. Thank you so much for asking. I will write the numbers so they are stacked. Can you tell us how you would solve it?”

Calvin explained, “Six plus two is eight and two plus two is four. The first time I got 82, but then when Jason said 48, I figured out I was wrong.”

I rephrased, “So you added the six ones and the two ones and got eight ones. Then, you added the two tens and the two tens and got 4 tens.”

“No. It’s just four. Two plus two is 4. The answer is 48.”  He beamed.  “Can you write my name next to it, like you did for the other kids?”

“Of course.”

I asked Jason if he noticed anything that was the same about his strategy and the strategy that Calvin used. Jason said, “we both decomposed the numbers. We both added the tens and the ones.” I asked Calvin if he understood what Jason meant. I motioned towards the similarities as Jason explained them.

 

 

 

Calvin smiled, “We both got 48.”

“Yes,” I agreed. “Calvin I am going to continue to write the problems horizontally, but I can also write them stacked, if you would like.”

“Yes,” Calvin replied.

This number talk took place about three weeks ago. I think about it a lot. I think about Calvin a lot. Usually, I get really angry when I think about Calvin. I’m not angry at Calvin. I’m angry for Calvin. Calvin wasn’t always in our district. He transferred here from somewhere else. Counting is challenging for him. His only experience with place value seem to be to “stack” numbers and use his fingers to tally up the digits in each column.

Calvin clings to stacking like a life boat. I picture him, tethered about 100 feet off shore, clinging to the lifeboat because no one taught him how to swim. I imagine, and maybe I’m wrong, that no one taught Calvin how to swim because they firmly believed that he couldn’t learn how to swim. They probably thought it was safer for Calvin to just cling to his lifeboat.  I can imagine the types of conversations that happened in regards to Calvin’s potential for learning:

“Calvin is just so low.”

“Calvin just needs to be taught a procedure. He can’t think ‘like that’.”

“Poor Calvin. His life is so hard. It’s not his fault, but it makes sense that he is so far behind.”

“Calvin can’t be in class with his peers. He is just so far behind.”

“Math just isn’t Calvin’s thing.”

“Calvin should be tested.”

Bullshit.

Who the hell are we to decide what Calvin can’t do? Maybe it isn’t Calvin’s problem. Maybe it is our problem. Maybe we need to ask ourselves, what can we do to help Calvin think deeply about mathematics?

After this number talk, I added stacking to our anchor chart of strategies. The week following this number talk, I wrote the Number Talk problems both vertically and horizontally. If I forgot, Calvin grinned and politely reminded me.  Gradually, Calvin stopped asking for the numbers to be stacked. He still clings to his strategy, but he seems to be thinking about trying to count up by tens. Yesterday, we checked in on his counting skills. Look at his work and ask yourself, what CAN Calvin do?

Calvin can count forwards and backwards by tens, off the decade! He might not be able to do it all the time, but he can certainly do it. Now, we have to help him develop his place value understanding and connect it to what he knows about counting.  I have been carefully observing Calvin during class lately. Here are some other things he can do:

• Calvin notices patterns when we do choral counts.
• Calvin always raises his hand when I ask if anyone wants to defend a solution.
• Calvin takes risks. Yesterday, one of Calvin’s peers used a compensation strategy to solve 19 + 19 = ______. Joey said, “I took one from the 9 and gave it to the nine in 19 and then I had 10+10+10+8 so I got 38.” I asked if anyone else could explain what Joey meant. Calvin’s hand shot up.  He had a big smile on his face. I called on him. He thought for a while, smile never disappearing. He said, “I am not really sure.” I offered, “help or time?”. He asked for help. He loves being in charge of choosing who gets to help him.

Let’s start looking at all of our students in regards to what they can do. Let’s stop finding excuses for why we can’t teach students. Calvin is far behind his peers.  He didn’t have the exposure to the math practices that his peers had, but Calvin has potential. Calvin has a voice. Calvin is capable of greatness. I will admit that Calvin terrifies me because it is going to require a lot of work and reflection for me to figure out how to help him think deeply about mathematics. I have a ton of questions:

• Should I give him place value blocks during the Number Talks?
• Should I give him Digi-Blocks?
• What if the other kids want to use them? Will it lower the cognitive demand of the Number Talks?
• How do I help Calvin connect counting to place value?

I don’t know exactly how to how help Calvin. I have a lot to learn about supporting K-2 students. So, I read. I try things out. I reflect. I ask for help and feedback.

Today, I tried to help Calvin, and the rest of the class, understand Joey’s compensation strategy. I put nineteen place value blocks in each of my hands. I asked Calvin to count them to make sure I was correct. Thank goodness he did because I was one short.

Then, I asked the class if anyone could use the blocks to show us Joey’s strategy from yesterday.  Ben volunteered. Ben picked up one of the cubes from my left hand and said, “Joey took one away from the nine,” he placed the cube in my right hand, “and he gave it to the nineteen.” Calvin watched carefully.  He looked up at me and said, “That’s a ten! We can trade it for a stick!” I smiled and asked him if he would like get the ten stick for us. He did. When he came back, he said, “that makes three tens. So it is 38!”

I said, “your darn right it is,” and I gave him the highest of  high-fives.

All of our students deserve respectful, engaging, math instruction that requires them to think deeply.  How can you help make this happen?

Kindergartners simultaneously terrify and inspire me. They terrify me because they are so candid and unencumbered by humility. They won’t hesitate to look you right in the eyes, in the middle of a conversation, and say, “this is boring.” They inspire me because their sense of wonder is raw, and, also unencumbered. Five year olds wonder as naturally as they breathe. Being curious isn’t something they have to practice or strive towards. It is just what they do; breathe, sleep, eat, be curious.

Once a month, I meet with Deb Hatt, one of our building based math interventionists, and Katie Reed, a Kindergarten teacher. We co-plan and co-teach a Counting Collections routine. We are trying to learn more about how Kindergartners record their thinking and justify their reasoning. We have so many questions:

• What is the difference between “how did you count?” and “how do you know your answer is correct?”
• What do Kindergartners understand about the word, “prove”?
• How do we honor student thinking while also nudging it forward?
• What is the difference between a “nudge” and a “shove”?

During our last planning session, Mrs. Hatt and Mrs.Reed discussed a recent blog post by Heidi Fessenden.  They were so appreciative of Heidi’s honest reflections about how she let go of some control in order to make space for the opportunity to learn about her students. Earlier in the year, I had shared some resources from Kassia Wedekind. We have found them incredibly helpful. Mrs.Reed encouraged us to try Kassia’s guide to conferring during our routine today. We discussed places that we might try to nudge student’s thinking.

Katie wondered, “What kind of questions should we ask that might nudge the students?” We decided we could start by just saying, “I noticed (something about how they counted). I wonder how you are going to record that?”

We knew it was still a challenge for many of the students to accurately record their count with a picture. Most of them had no problem recording the number they counted, but they were still struggling to show how they know their answer is correct. Some of them have started to record how they counted, but aren’t necessarily depicting an accurate number of objects. The last time we did this routine, I asked one of the students if she had drawn a circle for each one of the shapes she had counted. She looked at me, exasperated, and said, “No. You told me to show you how I counted, not how many I counted. This is how I counted, see?” She touched one of the shapes and then touched one of the circles she had drawn. “This (shape) is this (drawn circle).” A few students are pretty content to count the objects, write a number, and move on. Mrs. Hatt, Mrs. Reed and I have spent a lot of time thinking and talking about how we can help Kindergartners find a purpose for proving to themselves that they counted correctly.

Katie started the lesson by reminding the students about the Counting Collections routine, “We are going to do our counting collections routine today. Do you remember? We have some collections that we count and then we talk about how we counted. Today we are going to spend some time exploring how we can tell we have the right answer.”

She and Mrs. Hatt made a space for themselves on the floor, in front of the students.  Katie continued, “We have some shapes that we are going to count. Mrs. Hatt is going to count them first. Then, I am going to try. We are going to see if we get the same answer because, sometimes, when we are counting, we get different answers. Has it ever happened to you, when you are counting with somebody else and somebody else gets a different answer?”

A sympathetic chorus of “yes”.

Deb shook the shapes onto the carpet and counted. She waved her finger over the pile as she quickly and haphazardly accounted for each of the shapes. “I got 21,” she told Katie, “Now, you count them.”

Katie pulled the pile of shapes into her space and began to count. She got a different answer than Mrs. Hatt did. The children were riveted. Listen.

 

Mrs. Reed still wasn’t sure what the answer was so she decided to check again.

 

At this point, Mrs. Hatt and Mrs. Reed agreed that they had 19 shapes. Deb held up the recording sheet and asked the students how she might fill it out.  “It says, ‘how do you know?'” She wondered, “How do I know?”

Several students responded, “Because you counted them.”

Deb described how Katie’s arrangement really helped her see that there were 19 shapes. She drew a sketch of the group of ten shapes and the group of 9 shapes. Then, she asked the kids about the representation she drew on her paper. “Does this drawing look kind of like Mrs. Reed’s arrangement?”

“Yeah. It needs one more to make 20.”

“That’s right,” Mrs. Hatt agreed, “My drawing also needs one more to make twenty.” She asked the students if they could tell, by looking at her paper, that there were 19 shapes in her collection.

 

Katie introduced the visual anchor charts that we got from Heidi’s post. Deb introduced the tools; cups, ten frames, plates, and hundred charts. She reminded them,
“You are welcome to take anything that is up here. You have lots of choices.”

The kids went off to count.  Katie, Deb, and I circulated and watched. After a little while, I decided to check in with Alissa.  I reminded myself to take the time to notice what Alissa had done before I attempted to nudge.

I said, “I noticed that you were drawing lines on your paper, instead of drawing the shapes, is that right? Am I correct about that?”

She nodded yes. I continued, “It looks like you wrote that you have 17 shapes. I am wondering how do you know that the lines on the paper match how many shapes are in the bag?”

Alissa responded, “because I counted. I looked for the number 17 on the number chart.” She pointed to the 17 card sitting on the table. She had taken it out of the hundreds chart and used it to record the number on her recording sheet.

I decided to nudge a little bit. I asked, “What if someone came over here and said, ‘I don’t think there are seventeen shapes in that bag. Can you show me how you know there are seventeen in there?’ What if I said that? What would you show me?”

Alissa dumped the shapes out of the bag and placed them in the cup, one at a time, as she counted out loud. This time she counted 29. Then, she counted a third time, and got 19.  She chuckled and said, “I counted wrong.” I wondered how we could figure out which count was the correct one. I think at this point, I transitioned from “nudging” to “shoving”.  I was grasping at straws; “how can we organize?”, “can we make groups?” Alissa would humor me with a glance in my direction, then go back to counting. Listen to me fumble. Can you hear me sweating?

 

Did you hear what she said at the end? She said, “I need another one.” She filled up one of her ten frames. Then, she wandered across the room to the table with all the tools on it.  When she got back, she picked up right where she left off. I decided maybe I should go back to noticing, instead of shoving, so I attempted to be a mirror for her. I was pretty enthusiastic. Maybe too enthusiastic?

 

I don’t know if I did the right thing. I wanted so badly for Alissa to convince herself she was right. I wanted her to trust her intuition. She knew it was 19. I could tell. How could I get her to show it on her paper?  I knew I had to wrap it up. This conference with Alissa had lasted at least three days (or ten minutes).  Ethan was waiting patiently to show me what he found out. After Alissa changed the number of items on her recording sheet, I asked her how she was going to show that she knew the answer was 19?

I asked, “What if someone came over and said ‘I had bag L and I got 17. I think it is 17.'”

She responded, “Then I would say, ‘Okay. Let’s just do another one.'” She was just going to consent to 17. Oh no! After all this work, she was just going to consent to 17! I started nudging (shoving?) again. I said, “How could you convince them? What if you said ‘no. I am pretty sure it is 19.’ and they said, ‘well show me your paper. Show me how you know it is 19.’ What would you write on your paper. How did you figure out that it was 19?”

She said, “A ten frame.”

“Okay,” I gave one last push,  “so what could we put on your paper to show that? Think about that, okay Alissa. Think about how you are going to show here that you know it is 19. I am going to check in with Ethan and then come back and see what you came up with.”

I didn’t get a chance to check back in with Alissa before the closing circle. When I look at her recording sheet, I can tell she changed her thinking. She tried to erase some of her earlier lines. She still has more than 19 lines on her paper, but do those top two sets of hash marks resemble groups of five? Might that be a group of ten?

I don’t know. I have so much to learn about conferencing, but I am so grateful for my time with Alissa. She taught me a lot:

• Noticing is really important. Maybe more important than nudging?
• I can always go back to noticing, even after I try a nudge.
• A nudge can linger.

I really enjoyed using Kassia’s recording sheet. I would like to try noticing and nudging with all my students, K-12.

 

Kindergartners remind me that deep learning takes time: intuition isn’t built in one day.