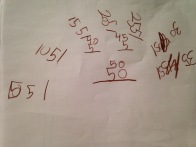For the last few weeks, I have visited a third grade classroom every afternoon. I love this time because I get to work with a teacher for whom I have a tremendous amount of respect. I wrote about her here.

This teacher has often told me how much she loves to teach math. She has been teaching for thirty years and she is always growing and learning.  She often comments about how much her math instruction has changed over the last ten years.  She has become an expert at honoring student thinking, valuing mistakes as learning opportunities, and cultivating perseverance.  She told me in the beginning of the year that she was worried about math this year.  She has a group of students who have so many social and emotional struggles in their lives that she is not sure how she will be able to get them to build their stamina for problem solving. She invited me into her classroom and I was honored to accept.

Admitedly, I was nervous.  I am great at “talking the talk” when it comes to teaching kids how to persevere and communicate their reasoning, but “walking the walk” is really hard. This teacher “walks the walk” so well and she does it with patience and love.  I knew I would be learning from her, but I was not sure that I would be bringing anything new to the table.

Awhile ago, I had read about the Hundreds Face challenge and thought, “That is so cool. I am going to try that with kids.”  Then, I filed the idea with the thousands of other amazing ideas that I have seen on Twitter and WordPress in the short 6 months that I have been spiraling through the MathTwitterBlogoshpere. The beauty of the #MTBOS is that, yesterday,  I found myself reading Malke Rosenfeld’s post, #HundredFace Round 2 and thinking, “Oh yeah. I remember that. That is so cool. I am going to try that TODAY with the third grade class that is struggling to persevere.”

I was still nervous.  What if they didn’t get it?  What if they gave up?  What if they didn’t want to make faces?  Should I let them build other things?  If I did, what would the constraint be?  I decided to ask Malke for her thoughts.  Here is another beautiful thing about the #MTBOS – you can ask far away people for help.  At 10:31, I posted some questions on Malke’s blog.  At 11:56, Malke responded with some suggestions and a few more questions. At 12:30, I responded with my new ideas. At 1:15, I taught the lesson.

Stop for a second and think about what I just said.  Now, think about this:  I have never met Malke. This was the first time that we ever communicated.

When I got to third grade, I told the third grade teacher my idea.  She was thrilled.  “That is a great idea!” she said. Then, she took out her giant tote of Cuisinaire rods. As the kids came in and got settled, I caught her up to speed about what Malke and I had discussed. We anticipated what students would do and what we would look for to share with the whole group.

First, we took a page from Malke’s book and told the kids to explore with the rods.  We smiled as we saw several kids building stairs and then noticing that they could compose rods out of other rods. They told us that 10 whites equals 1 orange. Here are some of the other equivalent compositions that they built:

Next, I told them about the challenge. Malke, the teacher, and I had all agreed that starting with 50, instead of 100, would offer scaffolding without lowering the cognitive demand of the task.

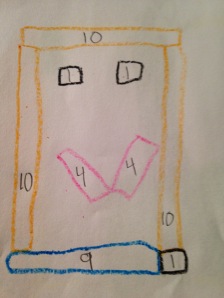
All of the kids started building faces.  Most of them were thinking about how to make the face equivalent to 50 white cubes. At this point, the third grade teacher and I agreed that our priority was to encourage students to stick with the task for as long as they could.  It was okay if some of the faces didn’t equal 50. We could come back to the faces next week and explore the math more deeply.  Here are some of the 50 faces:

The one on the right is one of my favorites. When I first approached the student, I asked him how he knew that the face was worth 50? He wrote, “blues are 9 so I need 5 ones.” I don’t know if you can tell from his picture, but he used 4 blues to outline the face, 1 blue for the mouth, and then he tacked on a white cube to the end of the mouth.

Some of the kids were struggling with making a face that was equal to 50 and some of the kids were done and ready for more.  The teacher and I conferenced and decided to offer a choice for the next challenge:

• Choice 1:  Build a face that is equivalent to 100!
• Choice 2:  Design your own face and tell us how much it is worth.

We weren’t sure if the second choice would offer enough of a constraint, but we think it did. The students who chose to design their own face were constrained by justifying the value of the face they had created.  The additional constraint of defining a value was beyond their zone.

Here is a sample of two students who designed their own face and told us the value.

 

And here are some of the #Hundredfaces:

 

 

There are still some faces that we need to revisit next week. I love these faces, even if the math is a little off:

The best part of this lesson was at the end. We asked the students what they learned today. Here is what they said:

• “Math can be fun!”
• “Never give up! You’ll never figure your way through it and you won’t learn if you give up.”
• “We made a bunch of mistakes today so our brains must have grown.”
• “Keep going – it’s a challenge.” (This one is from the boy who looked up at me half way through the lesson and said, with a big grin on his face, “This is so much harder than I thought it would be.”

And my favorite one…

“I learned to keep trying. I was trying to make a face with only 50 and I kept getting over 50 ,and over 50, and 0ver 50. I just kept trying the 50 face. Then, I got 50. Now, I am trying to build the 100 face.”

Thanks Malke.

This weekend, when I looked at my calendar, I realized that I had double booked myself for Monday. I was supposed to spend the whole day with the seventh grade math team AND I was also supposed to teach a 6th grade math class.  I thought about canceling the math class, but I really didn’t want to do that to the kids or the teacher I have been working with.  I decided I would just let the 7th grade math team know that I had to leave for an hour to teach 6th grade math.  I knew they would understand.

Then, halfway through my Sunday morning planning session, my kids started fighting, the dog ran away, and I realized that no one had eaten anything yet.  THAT never happens. Fast forward to the ride to school on Monday and I am panicking because I only have half a lesson planned. I also only have half the 7th grade math meeting planned.  One half plus one half equals a whole lot of random unfiltered blah bit e blah from me as I try to fake my way through the day.  Then, I had an idea.

What if I invite the 7th grade math team to join me as I teach the half planned 6th grade math lesson? Then, they could give me feedback about whether my lesson was only half a failure or a complete failure.

Fixed mindset voice in my head: Seriously, Sarah?  Why would you invite teachers to watch you teach a lesson you are so completely unsure about?

Growth mindset voice in my head: They could help me.  We could do it together.

Fixed mindset voice in my head:  And if it doesn’t work?  If you make a bunch a math mistakes, or worse yet, teaching mistakes?

Growth mindset voice in my head: I will just tell them up front that I am not sure about the lesson, I need their help, I only want specific feedback, and I am nervous about making mistakes in front of them.  Maybe I will ask them if they see me making a mistake, could they frame it as a question?

Fixed mindset voice in my head:  This is NOT a good idea.

Growth-ish mindset voice in my head: The worst thing that can happen is that I end up under the table crying.

Fixed mindset voice in my head:  Actually, the worst thing would be if the kids are totally confused because I didn’t get to take the time I needed to try all the math and anticipate what students will do.

But, what if I just say that to my peers.? What if am transparent?  Won’t the lesson inevitably be better if I have my peers help me analyze my half-plans before I go in to class, assist me as I navigate the nuances of students grappling with new concepts, and debrief with me afterward?

Yes.  The lesson will most definetly go better if I collaborate with my colleagues.

So I did.

When I got to the seventh grade meeting, I explained the situation.  I invited the 7th grade math teachers to join me in 6th grade math and then I waited.

Would they even want to do this? Some of them only teach 7th grade math?  What was I thinking?!??!? Why would they want to teach with me?

Silence.

“That sounds fun.”

“I would love to do that.”

Wait. What?

I continued to explain why I wanted their help and that I was really nervous about this experience.  I have had many elementary school teachers observe and teach with me, but being observed in a middle school math classroom was new territory for me.  I listed off all of my criteria:

• I only want feedback about posing purposeful questions
• I want you to use this “look for” sheet that I made and I want you to write specific evidence.
• I want your help.  I might ask you for suggestions in the middle of the lesson.
• If I make a mistake, please don’t point it out in a really obvious way. Ask me a question that prompts me to check my reasoning.

AND

• I need your help planning the lesson before we go in.

They were all in.

I shared how I wanted to introduce the tape diagram as a tool for creating equivalent ratios.  We had been using tables, interlocking cubes, and some equations.  I said, “I don’t want to force the tape diagram, but I want to share it as a possible strategy.  I don’t want everyone to have to use it.” I shared the Bubble Juice recipe that I had created as a context for us to work with:

Recipe for Bubble Juice

Makes 6 cups

4 cups juice

2 cups bubbly water

Then, we brainstormed:

• What is a tape diagram?
• How does a tape diagram keep track of the unit?
• How does a tape diagram relate to a table?
• How does a tape diagram relate to the interlocking cube model?

We didn’t have much time to plan, but it was enough for me to establish a feeling of trust: we were in this together and the focus was on learning from and with each other and the students.

When we first started the lesson, all the visiting teachers sat in the back of the room. That didn’t last long.  When I asked the students to create a ratio from my recipe, some of them were struggling.  I took a teacher time out.  I asked my peers, “Can you help me?  I don’t want to do the thinking for the students, but my questions aren’t helping.” One of my peers joined me.  One by one, my colleagues got up and integrated themselves into the class.

The rest of the class followed a similar rhythm.  I would pose a question to the students and/or my peers and we would navigate the learning trajectory together:

Me to my peers: “The recipe was the warm up problem.  I was going to move on to a problem about running laps. Do you think I should stick with the recipe context?”

Peers:  “Yes!  Do you want to make sure they have found all the different ratios in the recipe?”

Me to my peers: “Yes, but I don’t want them to just name them.”

Peers:  “Well. You have some listed on the board.  What if we  label the ones on the board with letters and ask the students to write down a letter that is an example of a part:part ratio?”

Me: “Yes! They can work with their table partners to come to consensus.”

Students: (having already heard the directions) “There is going to be more than one answer. Should we find them all?”

And this is how the rest of the class went.  All of us learning together.  In fact, when it came time to introduce the tape diagram, I handed off the marker to one of my peers.

“Sherri, would you mind explaining how you use a tape diagram to create equivalent ratios?”  She did.

Then, we asked the students, “How many cups of bubbly water and cranberry juice would you need to make 60 cups of bubble juice?”  Again, we circulated.

Toward the end of the lesson, I called a teacher team huddle.  I said, “One of the things I am trying to work on this year is the closing of the lesson. I want to take the last 5-10 minutes to encourage kids to connect what we did today.  I want them to walk away thinking and making connections. What should I ask them?”

• “What about, ‘How would you be able to find the amounts of bubbly water and cranberry juice needed to make any # of total cups of juice?'”
• “Or we could ask them why an answer is incorrect. ‘So and so said you would need 30 cups of cranberry juice and 30 cups of bubbly water, but that isn’t correct.  Why wouldn’t 30 and 30 work'”

We decided to ask both.  One of the students closed the class by sharing,”It can’t be 30 cups of cranberry juice and 30 cups of bubbly water because that would be too fizzy.  You have to keep the amounts of cranberry juice to bubbly water so they match the “juicey-ness” of the original recipe.”

I couldn’t have said it better myself.

So, it turns out, the lesson was 100 times better with my peers in the room.  Kids benefited. I benefited. My peers benefited.  Collectively, we magnified the learning.

The best part?  When we got back to our 7th grade meeting, after we debriefed, everyone agreed that we need to do this at all of our meetings.

 

 

 

 

 

I am part of a group of inspiring K-12 teachers in my district who just embarked on a crazy yearlong professional development journey together.  We designed a collaborative professional development certificate that will earn us the equivalent of three credits for re-certification.  Here is our plan:

We are going to meet monthly to choose a task that has a low floor and a high ceiling.  We are going to do the task together and anticipate what our students will do and how we will push their thinking without stepping on it.  Then, after we do the activity with our students, we are going to blog about it.  Before we meet next, we will all read each other’s blogs.  Next month, we meet again and start the cycle again.  Who are we?

• A District Math Coach
• A Life Skills Teacher
• 2 Middle School Math Teachers
• A Middle School Special Ed. Teacher
• 3 Fourth Grade Teachers who teach in different Elementary Schools
• A High School Math Interventionist
• An Elementary School Teacher who teaches a combined 2/3 classroom
• An Elementary School Math Interventionist
• A High School Math Teacher

We had our first meeting this week.  We  all set up our blogs and Twitter accounts. We chose our first task from the fantastic math site, Math Pickle.

We chose to play A Little Bit of Aggression with our students.

After we played the game ourselves, we wondered :

• Is it an advantage to spread your armies out so they are not bordering each other?
• Is it good to put a high number of armies in the middle territory?
• If you put a big number of armies in the mix,  should you get rid of your armies quickly so you can go first?
• Does the first or second person always win on a certain map?
• Could you play with multiplication instead of addition?
• Could you use fractions of armies?
• Is there a rule you could use to determine how to win, given a certain board and a certain number of armies?
• Is it ever an advantage to put one army in a territory?

This is what we wonder about our students:

• Will they stay with it long enough to develop a strategy? 
• How will they decide where to put their armies?
• Should I introduce it as a whole class or in small groups?
• How can I scaffold it so my kids can access the reasoning part of the task?
• What happens to the student who doesn’t persevere when their classmate steps up and takes over?

My favorite part of our meetings, besides getting everyone into the blogoshpere of course, was when we all started to organically help each other plan.

“Could you use blocks for the armies so the kids could manipulate them easier?”

“You could introduce the game over a week – a little bit at a time to build anticipation.”

“We could ask our students, ‘what would you do differently next time'”

“Yes! Or maybe ask them to write down questions they are thinking about as they are playing.”

“Or what if you paused throughout the game and asked them what they notice and wonder.”

“How did you decide where to put your armies?”

“Maybe you could make a bigger game board – like poster size”

Finally, I asked them, how does this activity fit in with math?

Somebody said, “It build perseverance.” Yup. “It also builds community because they will be talking about their reasoning.”  Hmmmm. Building community by talking through our reasoning. What a fantastic idea.

 

 

For the last two weeks, I have been mulling over my first blog post of the year.  Every time I sat down to write, it felt clunky and half true.  I didn’t blog much this summer. I tried to write about the fantastic experience I had working with K-12 educators in my district, but I fell short on the follow through.

At the end of the first day of school, I read Tracey Zagar’s provocative post about what NOT to do on the first day of school.  As always, she made me think about whether my beliefs and practices are aligned.  Part of my job is to coordinate curriculum for our district.  Several years ago, I pushed hard to get us to collaboratively design curriculum, instead of purchasing a textbook or program. Prior to the adoption of the Common Core Standards, our four elementary schools were each using a different outdated textbook as their math “curriculum”.  I saw the transition to new standards as an opportunity for us to work collaboratively to understand the standards and build a focussed, coherent, and rigorous curriculum around our understanding. It is really challenging for teachers to NOT use a math program, especially elementary school teachers.  There are several reasons for this, including limited planning time, shallow pedagogical content knowledge, and a disconnect between their own math identity and the identity cultivation that needs to happen in math classrooms today.  I am not blaming or judging teachers, at all.  This is just the current reality of education.

In the last few weeks, I have had the pleasure of teaching, planning,  assessing, and (most importantly) reflecting with a variety of K-12 teachers.  Throughout these experiences, I fluctuated between feeling sure and unsure.   In our district, for each of our units, we give a common unit assessment that was collaboratively designed.  For some units, if the standards are closely aligned with standards from the prior grade level, we give a pre assessment.  It is the same assessment that we give for the post assessment.  The purpose behind giving the pre assessment is to see what prior knowledge the students are bringing to the unit. What do they know? What are they still confused about?  How can we build on what they know?

In the second week of school, I met with the second grade teachers.  We discussed the common Unit 1 pre assessment that they had given the week before. Several teachers were overwhelmed.  They conveyed their worries about all the assessing we are doing – not just in math, but all subjects. They talked about how some of their students were overwhelmed by the Unit 1 pre assessment.  As I listened, I felt unsure.  I questioned all the work we had been doing in an attempt to create consistency in our math instruction. We created these unit assessments together in an attempt to understand the standards and guide our conversations about what it looks like and sounds like to meet the standards. We have also been doing learning rounds to focus on the standards of math practice.  Last year we started doing learning labs at some of our grade level meetings so we could teach and learn together in actual classrooms with live students. Were these  assessments hindering the work we had done on cultivating a math culture that honors inquiry and risk taking?

Then, I thought about the teachers with whom I am currently collaborating. In one of our buildings, the math specialist and 2/3 teacher are co-planning and co-teaching the 2nd graders. They have been using Jo Boaler’s week of inspirational math videos and tasks. They invited me in to teach one of the tasks. When I entered the room the day of the lesson, the students were scattered around the room. Many of them had headphones on to dampen the noise. Some were sitting on t stools or exercise balls.  All of them seemed to be engaged in what they were doing.  One of them looked up at me and said, “Mrs. Caban. I just made three mistakes.  My brain is growing!”  The teacher informed me that they were finishing up their pre assessments.  I commented that they didn’t seem worried or upset.  She said she told them that they may not know the answers to the questions, but she wanted them to give it a shot because if they tried, even if they got it wrong, it would help her understand their thinking.

Back at the grade level meeting, the same teacher asked her peers about one of her student’s work.  She was not sure if the student is demonstrating an understanding of this standard:

• CCSS.MATH.CONTENT.2.NBT.A.1
  Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. Understand the following as special cases:
• CCSS.MATH.CONTENT.2.NBT.A.1.A
  100 can be thought of as a bundle of ten tens — called a “hundred.”
• CCSS.MATH.CONTENT.2.NBT.A.1.B
  The numbers 100, 200, 300, 400, 500, 600, 700, 800, 900 refer to one, two, three, four, five, six, seven, eight, or nine hundreds (and 0 tens and 0 ones).

Here is my drawing of what the student did. I have been meaning to get back to the teacher and take a picture of the actual student work, but I just haven’t had time.

So, this wonderful group of second grade teachers proceeded to engage in a conversation about what this student knows about place value.  One teacher didn’t think he demonstrated understanding of the standard because he included the values of all the digits and the question specifically asked for the value of the 2 in the hundreds place.  Another teacher disagreed.  She said he is showing the value of the 2 in the 200.  I think at this point I may have asked them what this standard had to do with the other standards that they teach.  They started discussing decomposition and how it relates to work with addition and subtraction. The teachers asked, “What did the student do for the other numbers?”  (there were 4 different three digit numbers).  He did this for one of them:

Looking at actual student work is incredibly important.  It is essential if  teacher’s are going to calibrate their understanding of student understanding. The irony is:  I don’t have it.  BUT, you are looking at my understanding of the student work that I analyzed with my peers and that is what this blog post is really all about.

The above story is one of many similar stories that I could tell about my first three weeks of school.  I have met with every grade level in our district. At every meeting, we took out pre assessments, analyzed them, argued about them, adapted them, and used them to plan.  There is a lot about our common assessments that bugs me:  some are too long, some of the questions stink, it takes a long time to score them because we use standards based rubrics, and my least favorite thing: they are stressing some people out.

What do I like about them? We created them together and they evolve with us.  Here are some examples of how they have evolved this month:

• The first and second grade teachers decided to only give the interview section of the unit one pre assessment next year.  IF a students gets a “3” on the standard that is assessed in the interview AND seems comfortable with persevering, they will continue with the rest of the assessment. If not, they will use the information they get from the interview to plan instruction.  They said this will be less stressful and still informative.
• The 6th grade teachers seemed to enjoy watching a teaching channel video on one of the standards before we commonly scored.  They want to do more common scoring because it really helps them reflect on the implications for instruction and what changes we need to make to the assessment and rubric.
• The K-12 district interventionists want to devote some of our meeting time to making an assessment bank for the standards so teachers have a variety of vetted assessments to use to inform their instruction and measure progress.
• Next year, we are going to try to postpone any pre assessments long enough so more people can devote the beginning of the school year to using Jo Boaler’s week of inspirational math without feeling rushed.

I am not claiming that our assessment system is awesome. I feel pretty crappy that there are kids in our district who felt stressed out in math class, but I think the changes that we are making will be an improvement.  What is most important is that WE are making the changes.