A few weeks ago, I read Tracy Zager’s post about intuition. I also took the opportunity to go through her slides from her #CMC North presentation and push myself to think more deeply.  In an effort to understand the role of intuition in math thinking, I recorded my entire thinking process – all of my mistakes, questions, and partial understandings in this post. I kind of feel like I am about to expose myself.  I am making myself publicly vulnerable. This is not easy for me, but I am doing it in the interest of becoming a better math teacher and coach. Tracy has got me thinking that my job is to help students and teachers refine their math intuition. Therefore, I have to explore my own.  Here are my candid thoughts.  The picture on the left is a screenshot from Tracy’s slideshow (which can be found on her blog. Screenshots of my actual thoughts are on the right.

 

 

 

 

At this point in the exercise, things got really interesting.  I started to wonder:I followed my intuition both times.  When I listened to it, it helped me. Why did I get a closer estimate on the smaller pumpkin?

Was it because I have more experience carrying objects that are closer to 5 pounds?  Does it have to do with my question about weight distribution?  Is it because heavy objects all feel so “heavy” – there is less clarification for me about “how heavy”?

Reuben Hersh says intuition is a “trace in our mind left by our experiences”.  Was I less intuitive about my larger pumpkin guess because I have less experience with carrying things that are over 5 pounds?  Would a professional delivery person have had better intuition?

I think it is about those little voices, Tracy.  Most of my childhood schooling was spent listening to the voices of my teachers. I didn’t spend any time developing my intuition. I think I started listening to those little math voices when I first started teaching. I was in a one room school house ten miles off the coast of Maine. I was the new teacher and my students were in Kindergarten, third grade, and sixth grade. I had no idea what I was doing. I will forever be indebted to Thom Buescher, a G/T consultant from Camden who was hired  to help me figure out how to teach such a broad spectrum of learners. He suggested that the school board purchase the K-5 math program, Investigations in Number, Data, and Space and the 6-8 math program, Connected Math. So, they did. And I started opening up the communication lines with those little math voices who I hadn’t heard from in a very long time. I took those resources home and I did math, math and more math. I loved it.  I learned so much math the 6 years that I taught on Monhegan, but I only scratched the surface. I left Monhegan in 2007. Since then, the amount of math voices in my head has grown exponentially. 

However, I am finding, there are still a lot of communication lines with weak connections. Back to Tracy’s slideshow:

Now, I want to take a minute to remind you that you are looking at naked thinking. I am sharing screenshots of my  thought process. You are seeing all the nuances of how  I approached the problems in this slideshow. You are “seeing” me revise my thinking in my head. These notes have not been edited. While I took notes, I was intentionally trying to follow my own intuition and write down everything I thought, in an effort to see if I could find the communication “weak spots” in my own intuition. Watch what happens.

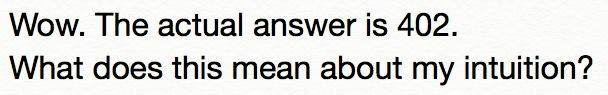
As I re-read these notes, I am fascinated.  I have always been a “rusher”.  I think too fast and it is not a surprise to me that I “saw” 4×4.  I wonder how thinking fast impacts my intuition. As a student, I wasn’t given the time to hone my intuition.  As an adult, I am realizing how important it is.  The good news is – somewhere in my head- there is a “slow down voice”.  Reread my notes above.  Can you hear it?  I think I would like to turn up the volume of that voice.

So, I continued to think about the other estimates on the slide.

So my “gut” knows why 6,700 isn’t reasonable, but I am really struggling to find the precise words to explain it.  Fascinating. When my intuition is strong, I struggle to explain it.

Try.

If I had 6,700 groups of 47, clearly I would have more than 6,739 because 6,700 x 47 is equivalent to 47 groups of 6,700 and 6,739 is barely over 1 group.  

Ha!! Did you see that? I think I just refined my intuition by having to articulate it. What did I refine my intuition of? Perhaps the relationship between multiplication and division? Maybe the magnitude of numbers?

150 is unreasonable because 150 x 100 is 15,000. (150 x 10 is 1,500)

Wait a minute. I don’t want to just move up a place value – don’t rely on old tricks – refine your intuition, Sarah!

(15 x 10) x (10 x 10) = 15 x (10 x 10) x 10

15 x (100 x 10) = 15 x 1,000

15 x 1,000 = 15,000 

Yes!

So if 150 x 100 = 15,000 than 150 is unreasonable because 150 x 50 = 7,500 because half of 100 is 50 so I need to cut 15,000 in half. 

So it has to be less than 150 and greater than  120. Aha! So the most reasonable estimate on the slide is 130.

Ha! I just got to the part of the slides that talks about externalizing my thinking and I have been doing it the whole time. 

Intuition is developed. Wow. 

Tracy goes on to to say “My intuitions are based on my knowledge and my experience. The more I have, the more robust my intuitions are likely to be.” I am thinking it is really important to connect this with the earlier quote from Erich Wittmann: 

So, as a learner, the key words are My. Me. I. If I want to hone my intuition, then the knowledge and experiences have to be mine, all mine.  What does that mean?  I think it means I have to make the mistakes, acknowledge the mistakes, articulate how I would correct the mistakes, and reflect on what I learned from the mistakes.

So is it just about mistakes?

No.  I think it is also about connections.  If I want to hone my intuition, I have to connect my experiences.  I have to wonder how everything fits together. You can ask me questions to prompt me to wonder, but it has to be me who does the wondering and it has to be me who makes the discovery.

In their book, Making Number Talks Matter, Ruth Parker and Cathy Humphreys say some provocative things about whole group sharing.  They say “Students are used to listening to their teachers’ explanations, and saying something once won’t hurt – as long as you don’t expect the students to understand just because you have explained it.  They need to make sense of ideas for themselves.”

They also go on to say:

“Currently, deciding the order of sharing based on the sophistication of strategies, from least to most, is a popular notion. Using this method, it is argued, allows the underlying mathematical concept to build. We have valiantly tried this approach at one time or another but generally take a more organic approach….preselecting an order for sharing or scaffolding toward our “best explanation” can take the agency right out of the hands of students and make processing time almost algorithmic”

Wow.  I recently posted this quote on Twitter because it really hit me in “the gut”. It spoke to me.  It was one of those little voices.  It connected a lot of other recent wonderings:

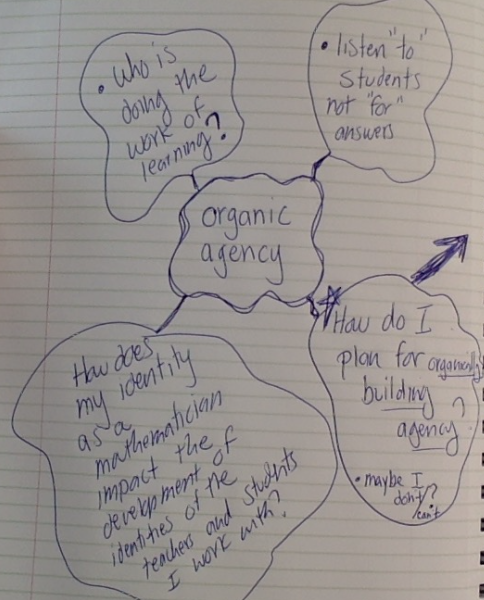
The Twitter post prompted a conversation about when and how to sequence student work. It prompted a great conversation about purpose and intention. As a facilitator,  I wonder, is it possible to sequence work AND hone intuition?  Is there a difference between organic sequencing and planned sequencing?  Am I facilitating opportunities for students to connect ideas or am I sharing ways that I connect ideas? When I solve problems as I anticipate student thinking,  am I taking the time to connect my ideas or am I just rattling off a bunch of different ways that students might use to solve the problem? Am I honing my own intuition or am I “planning my presentation”? Yikes. This is tough.

How do I balance honing and planning?  Is there a connection between honing my intuition as a math learner and honing my intuition as a math teacher?  Does the former inevitably impact the later?

In her slide show, Tracy prompted me to look through a series of questions that promote intuition, choose one from each category, and incorporate it into my teaching. My goal for 2017 is to take Tracy’s advice, but make a slight modification:

• I will incorporate the following questions into my teaching AND learning:
  • Forget about the question for a second. What’s going on in this situation?
  • Let’s refresh our memories about what each of these numbers represents.
  • Slow down. We want to follow your thinking. Can you tell us your reasons for approaching it that way?
  • How did thinking about your experience with __________ help you here?
  • What tipped you off that something wasn’t right?
  •  It feels counterintuitive, doesn’t it? Say more about that.
  • What’s making you doubt?
  • Did anyone change your mind today? How?

My favorite part of this goal is that I haven’t even read Tracy’s book, yet!! I am waiting for it to arrive in the mail. I am just finishing up Making Number Talks Matter.  I am really looking forward to continuing my “gut checks”.

In my last post, I shared an experience about trying to explore the properties of operations with K-12 teachers and students in order to understand the progression of how these properties are taught and learned.  Since then, so much exciting learning has happened – a lot of it has been mine.

One of the fourth grade teachers in our K-12 Professional Learning Group approached me to talk about her experience exploring some complicated expressions with her students.    She said she showed her students this expression, (7×8) + (8×3) and asked them what they thought the solution was.  You can read more about her experience on her blog, but essentially, this is how a few of her students approached the problem:

Chrissy was thrilled that her students were decomposing 7×8, but she was hoping they would see that you could recompose the factors into 8×10.  When she came to me, she said, “I got the students to see how you could combine 7×8 + 8×3 to make 10×8 and we talked about how “seeing” 10×8 would be so helpful because they know 10×8 is 80.”  Then, she shared something provocative.

She said, “one of the students, Emerson, said, ‘you can’t do that. You have to do what is in the parenthesis first.'”.

Wow.

“What do I do with that?” she asked me.  “What should I do next?”

“Great question. I am not sure.” I wondered what some of my colleagues on Twitter would recommend as a next step.

Wow. We got so much instantaneous feedback. It was awesome. We were still left with a lot of questions:

• Is there such a thing as the “reverse distributive property”?
• Is factoring out the 8 an example of “using the distributive property” or is it something else?
• How do we get these students to shift their perspective about decomposing factors so they can see the potential of recomposing factors? How can we get them to connect decomposing and recomposing?
• How do we get them to see and use parentheses as a tool instead of a rule?
• Is it possible to help them figure out that this “regrouping” only works when the expressions in the parentheses share a common factor?
• Will they, can they, figure out why?

We asked our Twitter friends for some advice about how to pursue these questions, our questions, and still honor Emerson‘s original disequilibrium.

David Weese actually started a planning doc so that multiple people could contribute to the brainstorming. You can see it here.

Christopher (@Trianglemancsd) suggested using a picture of Eggs!

We decided to ask the students, “what are all the different ways we could figure out the total number of eggs in the picture? Don’t tell me the answer. Just tell me all the ways you could find the answer.” Chrissy and I  didn’t have a ton of time to connect in person. We were connecting via Twitter, David’s planning doc, and short conversations in the hallway en route to and from the bathroom. This was all happening 24 hours before the last day prior to Thanksgiving vacation. I anticipated what the students might say. You can read about this in the planning doc that is linked above.

I emailed Chrissy and begged her to let me come in to math the day before Thanksgiving break to try this lesson with her kids. I told her I completely understood if she wanted to tell me to shut up and go on vacation already. She didn’t. She was equally as curious to see what her kids would do with this picture of eggs.  We didn’t have a ton of time to hone our plans, but  so we decided to jump in because we really wanted to revisit the topic before too much time had passed . Keep in mind, what you see and read below grew out of unrefined plans.  It is bumpy.  Chrissy and I are unsure at times.  I am sharing it with you so I can learn from the experience and so we can learn together.

We showed the students the picture of eggs and asked them to record ways that they could organize them to find out how many.

This is what they did:

This slideshow requires JavaScript.

Chrissy and I started a discussion by asking Chase to share his thinking.  The expressions below were written before Emerson asks her question.  You can’t see the video of Chase, but you can hear him. The black lines indicate what he was drawing on the smart board. The pause in the middle of the video is because the white boards kept falling off the ledge. Hence, my high pitched reminder of why I had suggested NOT putting the white boards on the ledge. #reallifeclassroom

Have a listen.

As I listen to him now, I wonder if I missed an opportunity. I got caught up in the fact that Emerson noticed one of Chase’s expressions didn’t match the image.  I didn’t catch the fact that he says, “and I would add those together.”   I wish I would have asked him what he meant by that.

At one silent point during the audio, Chase changed one of the expressions on his whiteboard from (2×4) to (2×3) and handed it back to me:

 

We only had 15 minutes before lunch.

“Emerson, it is because he is adding….”

Let her finish, Sarah!

It is so hard to listen to myself in this video. I want to jump through the recording and put my own hand over my mouth. I wish I hadn’t cut Emerson and her classmate off. The more I listen to and/or watch myself teach, the less I want to talk in a classroom. (This is a good thing!) I talk so much less than I did when I started as a math coach, and yet, I still think I talk too much.

At this point in the lesson, a few boys came in. They weren’t present at the beginning of the lesson so we tried to catch them up by explaining what we were doing.

Have a listen. This conversation is where we start to really wonder about the role of those parentheses.

 

As I listen to this clip, I wish I had prompted Gavin to tell me more about what he was thinking.   I was so focussed on getting these students to discover what I wanted them to discover that I missed a golden opportunity with Gavin.  I wish I had asked Gavin, “Why do you want to take the two out of the second set of parentheses?” (Tracy Zager, you’ve got me thinking about asking better questions to encourage relational thinking.)

I wish I could rewind and pause.  I was listening for answers instead of to my students. (Where did I read about this last weekend? On Twitter? I think it came out of the #CMCmath North conference? Was it Zak Champagne who said it? Whoever said it, it has really stuck with me.)

I wonder what would happen if I showed Gavin the video above, paused it, and asked him why he wanted to “take the two out”?

At this point, it was time for lunch. How many times have you been in the middle of some deep, messy thinking and the bell rings?  I wish I could have spent the whole day with Gavin and Emerson.  Interestingly, they hung around and chatted with me while everyone else got ready for lunch.  We continued our conversation for a few minutes.

As I reflect on this lesson, I think I  was rushing. I was so desperate to get Emerson and Gavin to figure IT out before the bell rang. 

What was I thinking? The IT is huge! Gavin and Emerson are wrestling with some giant ideas about the distributive property. They are wondering about the limits of parenthesis. They are trying to figure out when to add partial products and when to multiply them. They are manipulating expressions to match a context so that the math makes sense. This kind of learning doesn’t happen in 15 minutes or less. 

I was so worried about losing the opportunity to connect big ideas that I hurried right past several opportunities to connect big ideas.

It has taken me weeks, literally, to write this blog post. It takes me a loooooong time to process experiences because I have to understand all of “it” before I can make sense of parts of “it”.  See Pam Harris’s post about the three groups of people. I am a classic “c”.

I am so grateful for taking the time to process this post.  I used to think all of Gavin and Emerson’s thinking would disappear over Thanksgiving vacation.  I thought I had to be the super hero math teacher lady who swooped in and helped them organize their thinking in a neat and tidy pre-lunch math chat. 

Now, I realize that Emerson and Gavin are doing some serious thinking. I need to let them be the hero’s of their own math stories.(Thanks Dan Meyer for planting this seed.) It takes a long time to construct the understandings that they are wrestling with. They haven’t even started their multiplication and division unit this year. 

Wow. I need to say that again.

They haven’t even started their multiplication and division unit this year.

I wonder what’s on the menu for that unit?

How about eggs?  

Lots and lots of eggs.

 

About a month ago, I saw this in Twitter:

At first, I thought, “how would any of those problems be easy to do in my head?” Then, I saw an entry point.  I thought about multiplication as “groups” and I realized that I didn’t actually have to do a lot of complicated computing.  I could combine the groups to make friendlier numbers. I thought of 23 x 37 – 13 x 37 as 23 groups of 37 minus 13 groups of 37. That is equal to 10 groups of 37 which is 370.  All of a sudden, these problems seemed much more accessible.  I was able to solve the others in a similar way, except one.  I decided to reach out to @nomad_penguin, who originally posted the problems, to see if she could help me out.

 

Below, you can read our conversation, from left to right.

 

I almost edited out the part where I mixed up the problems, but I left it in because I think it is really important. Communicating math thinking is really hard.  I talk fast and think slow.  My mind is forever chasing my mouth and, in the case of Twitter, my fingers. I think it is important to share this because I need to remind myself that mistakes are incredibly valuable.  In this case, my mistake was not slowing down to think about what, exactly, I wanted to share with Aimee.  Thinking about what I want to share will help me think about what I currently understand and what I am still confused about. If I can’t clarify my thinking than I won’t be able to verify it.

I want to say thank you to Aimee.  I am so grateful that she supported my struggle. She didn’t tell me the answer, but she also allowed me the space to take a risk. I felt okay telling her that I was having trouble.

I decided I was going to share this problem set with the K-12 professional learning community that I am a part of. We had some really interesting conversations.  The elementary teachers used strategies that were similar to mine.  Many of them thought of “groups”. Robyn, one of the high school teachers in the group rewrote the problems as factored versions of themselves. I think her work looked something like this: (Robyn, feel free to correct me if I am butchering your ideas.)

23 x 37 – 13 x 37 = 37 (23-13)

37(23-13) = 37(10)

37(10) = 370

I asked Robyn, “what do you call that?”.  I can’t remember exactly what she said, but I am pretty sure she mentioned “factoring” and “the reverse distributive property.”

At this point, we got into a pretty lively argument about what, exactly, the distributive property IS.  Is it all of the equations listed above?  Is it just some of the equations listed? Can you “use” the distributive property without knowing that is what you are doing?  Is “using” the distributive property the same as “understanding” it?

We decided we wanted to learn more about the progression of the distributive property, and other properties of operations. We decided to try this activity with students at different grade levels. We realized that some of the teachers in our  group would not be able to try this activity as it is presented above because it would be beyond their student’s reach.  So, we brainstormed other problems that would still present opportunities to use other properties of of operations.  Here are some options that we came up with:

We all agreed to try one of these problem sets with our students and share what we found out via our blogs.  Our guiding question:

• What do our students understand about the properties of operations?

When we left the meeting, I was still wondering about a lot of things. I continued to let my questions simmer. A couple of weeks after this meeting, I read one of the teacher’s blog posts.  She tried the problems with her students and it was a really frustrating experience.  “Oh no!”, I thought. “What have I done?”

As I read her post, I wondered if I should have structured this professional learning experience a little differently.  I don’t think I had taken enough time to ground our conversations in a context.  When we discussed how we approached the expressions, we didn’t have an image to anchor our understanding. As much as I love Number Talks, I think I need to be more intentional about grounding some number conversations in an image so we can really connect the numbers and symbols to a representation. We need the image to explore the structure of our number system more deeply.

I decided I was going to think about a way to incorporate a number talk image into our next PLC meeting.  How could I use an image to get us thinking about rearranging expressions to show equivalence?

 

 

When I woke up this morning, I went right to Twitter to see if I could find video footage of the keynotes from the California Math Conference. I watched Fawn Nguyen and I  jotted down the things that made me think, “Yes! I want to do that!”.

Then, I watched Dan Meyer. He challenged me to turn a question into a story and put students at the center of it as the hero. I thought about that for a while. How do I draw a student into the narrative so she is the heroine – the owner of the learning? How do I give her the power?

Later in the day, I was exploring the geometry progression with a colleague.  We were playing with triangles and parallelograms in order to understand the first and second grade geometry standards better.  By accident, I created a small parallelogram and a large parallelogram.  I wondered if they were proportionate.  As we worked, I kept generating more questions about the situation. My favorite question was, is the area of  proportionate figures related to the scale factor?

I remembered Dan’s keynote. I wanted to make myself the hero of this story. I didn’t want someone to tell me the answer to this question. I wanted to figure it out.  My friend, who has taught high school math, was eager to help me make connections. I told her I wanted to “own” my understanding. I needed some think time. She respected  my wishes.

While we were exploring, another colleague approached me.

“How long have you have been a math coach?”

“5 years.”

“Oh. I noticed you were really excited about learning math. What is your background?”

“I taught K-8 in a one room school-house off the coast of Maine for 6 years. Then, I taught fourth grade for four 4 years.”

“What grades do you coach?”

“Well I started as a 3-8 math coach, then a K-5, now I am K-12. We have a really small district and my role has kind of changed and evolved over the years. We also have math specialists in all the buildings, including one in the high school.”

“I only ask because sometimes it is hard for generalists to become math coaches because they don’t have the content background. You work with high school teachers?”

“Well…. yes. We work together. I ask them questions about HS standards.  Sometimes they ask me questions about the K-8 standards. My role is to be a conduit.”

My cheeks felt like they were getting red.  I wondered if other people were listening. I quickly started packing up my things. I wanted to hide all the pieces of scrap paper with my notes on them.

I nodded and smiled.  I said, “I just really enjoy learning math.”

Ouch. I tried not to feel it, but it seeped into me before I could stop it.

Shame.

I don’t even like typing that word. It is the worst feeling and to feel it about a subject that I have finally grown to trust again…… It just sucks.

I wanted to shake it off. I wanted to forget about it. This person doesn’t know anything about me. Later, I thought about all of the things I could have said to this person. I thought about all the qualifications that make me a good fit for my K-12 coaching position.  I almost started listing them here, but my qualifications aren’t what this story is about. This story is about how shame got in the way of me becoming the hero of my own math story.

If I wasn’t still feeling ashamed, I would probably describe my favorite question  in more detail. I would stay up until 2:00 am pouring over my notes from today, in an attempt to articulate my current understanding of how area is and isn’t related to the scale factor of proportionate figures.  I would share all the mistakes I had made. I would ask more questions. I would try to connect my thinking to all the standards.

I don’t really feel like doing any of that right now.  The shame has gotten in the way.

When I was grappling with my questions about proportionate parallelograms,  I felt empowered.

How did those words,

“You work with high school teachers?”

take me from feeling empowered to feeling ashamed in a matter of seconds?

Was it because I felt vulnerable?  I thought vulnerability was a good thing.  When I am vulnerable, I am open, unassuming, ready to learn.  When I was exploring my favorite question with my colleague, my vulnerability pushed my thinking and fed my curiosity.   It allowed me to take a risk, to explore something that I wasn’t totally sure of.

Suddenly, when confronted with a question about who I work with, vulnerability was not so good. It meant I was weak.  I didn’t have the “right” experience.

It ignited shame.

I am not sure what I want to do with this experience.  I am not even sure why I am sharing it. I guess maybe I hope that if I acknowledge the shame, I will take away its power.   I can’t help but wonder, would this person have asked the same question to a high school teacher who told him that she was coaching elementary teachers?

I used to think that being vulnerable was my strength. It was at the heart of the relationships I have built over the last five years.  It was where I tried to start every day. It was what allowed me to feel so comfortable, and even excited, about saying,

“I don’t know.”

Now, I am not sure.

Unfortunately, vulnerability doesn’t have a switch.

Fortunately, I will learn from this. I will think about the teachers and student I work with.  I will continue to value and protect the space where being vulnerable can be empowering.  I will encounter more situations like the one I just described.

Maybe, after some time, I can get myself to a place where I can say,

“Yes. I work with High School Teachers. And they work with me.”