Recently, a middle school math interventionist came to me with a problem.  She has a small group of middle school students who she teaches every day.  She worries a lot about whether or not they like math. She says they don’t persevere.  She wants them to enjoy problem solving but they give up so easily. I asked if I could join her in class one day so I could experience, first hand, the dispositions of her students.  She welcomed me with open arms.

At this point, I wondered, what is my purpose?  Clearly my purpose was not to miraculously, in sixty minutes or less,  get these students to love math and see themselves as vital contributors in a math community.  Right?

I was pretty sure these students knew that they struggled with Math.  I don’t think they needed me to point that out.  I wondered if it would be worthwhile to ask them about their struggles. Maybe we could identify some times that struggle could be helpful.  I decided to keep an open mind and try to do more listening than talking. The cool thing about my job is that I work K-12 and I have worked K-12 for the last 5 years. So, when I walked in to Miss. R’s  math class, I was greeted with ,”Hey Mrs. Caban.”  I have known these kids since they were in third grade.

I wrote on the board:

I asked them to talk to me about anything in their lives that they struggle with.

Right away a boy said, “Football.”

I asked, “Can you tell me some more?”

“I love football. When I make a mistake on an important play, it is hard for me.  I screwed up the play.”

“So making a mistake in football is a struggle.”

“Yes.”

“Anyone else have something you struggle with?”

Three different students started talking at the same time.  I asked if we could take turns because I really wanted to hear everyone. First I called on Ashley.

“I struggle when I am reading a really good book and the character dies. I know it is essential to the development of the plot and usually important to the theme, but it is still so hard. Usually, I cry.” She chuckles to herself, “It is just so hard.”

“Thanks for sharing that, Ashley. I totally agree. Sometimes when a character dies, it is like I lost a friend. What else do you struggle with?”

“Friends.”  Charlotte said, as she glanced at Joanne across the room.

“How so?”

“Well, sometimes, friends (another sideways glance at Joanne) assume things about you that aren’t really true and they don’t ask you so they don’t really know.  People shouldn’t make assumptions about other people.”

“Wow. I agree that friendships can most definitely involve struggle.  What do other people think about this?”

Lots of agreement.

“Joanne, did you want to add anything?”

“Yeah. I struggle with not being able to see my family and friends a lot because they live far away. I miss them.”

“That is hard.”

Finally, Eve said, “So are we not doing math today? Are we just going to do counseling?”

Chuckles.

“That is such a good question, Eve. What does struggle have to do with math? Before we talk about that, though. I have a different question for you. What does struggle look like and sound like?  Tell me what struggle looks like and sounds like.” Here is what they said:

 

Then, I put a continuum on the board and asked them to place their struggle on it.

<——|—————————————————|——–>

No struggle at all                                                                                              Struggle all the time

They discussed which of their struggles were more challenging and why. Then, I asked them, would it be better if we never had to deal with struggles?   They unanimously agreed that it would not be better. I asked why?

They said struggle can be good because it is necessary, it helps us learn from mistakes, we get through it and build confidence, and we become better communicators.

“So… do you ever struggle in math?”

“Yes.”

“I do too.  I was wondering if I could share a struggle with you and you might help me with it. I have been thinking about a problem, but I don’t know the answer. I want you to help me solve it, but I can’t tell you if your answers are correct or not because I haven’t solved the problem yet.”

“What do you mean you don’t know the answer?  How do you not know the answer?”

“I don’t know the answer because I just invented the problem and I haven’t solved it yet. I thought I would present the problem to you and see what you came up with.  Do you want to try it?”

“Sure.”

“Okay. Thanks. So here it is.  Yesterday, I was in a second grade classroom. The teacher was giving her students pieces of fabric and asking them how many peace signs were in each array.  I don’t have the fabric with me because she wasn’t able to let me borrow it. She is still using it in her classroom.  I took some pictures of some of the pieces. They looked like this:

Right away, one of the students said, “So, you want us to do a second grade problem?”

“No. Not at all. The problem is one that I made up.  As I was looking at all these pieces of fabric, I wondered whether it was possible to sew them all together into one big rectangle, without changing the pieces. I wondered if I would be able to match up all the arrays to make a rectangle. I don’t know if it is possible. I thought you could help me figure it out. I don’t know if there is a solution or not. That is going to be the tricky part.”

“You really don’t know?”

“Nope.”

When I was planning this lesson, I thought a lot about Tracy Zager’s NCTM Ignite talk: Going Beyond Group Work. My favorite quote: “They (Julia Robinson and Yuri Matiyasevich) managed to do all this fantastic collaboration without a teacher saying, ‘okay Hilbert’s tenth is going to be a group project.'”  I reminded myself not to squeeze the life out of this organic problem that I had stumbled across. In her presentation, Tracy challenged us to teach our students to “collaborate in ways that are fluid and powerful”.  Yikes. In order to do that, I might have to give up some power.  That sounds scary.

I explained to the students that I wasn’t able to bring the pieces of fabric, but I was able to use graph paper to cut out pieces that were the same size as the ones in the photo.  I only had time to make 4 sets of graph paper arrays.  There wasn’t enough for everyone to have a set.

“Can me and Liz work together?”

“I want to work by myself.”

“Me too.”

“Me and Jon can be partners.”

And there you have it.  Within 30 seconds, these students had organized themselves: some into thinking partnerships, some not.

They all  jumped right into the problem.  Some were moving the graph paper pieces around. Some were looking at the picture of the fabric pieces. All were engaged in problem solving.

They were acting like mathematicians.

• They were asking questions:  “Does it matter how long the sides are?  Is there more than one way to do it? Does it have to be a long skinny rectangle?”
• They were sharing observations: “Hey! A lot of these rectangles have a side length of six. Let’s try to match up the sixes.”
• They were critiquing each other’s thinking: “That won’t work because you will end up with a tail.  You have to combine the rectangles so you can line up their sides.

As they worked, the excitement built. The kids were frantically moving graph paper around.  Every few minutes, somebody would ask me, “are you sure you don’t know the answer?  What if it isn’t possible?” They never disengaged from the problem solving.  They didn’t even look up.  They just asked the questions. I can’t say for sure why they kept asking, but I can speculate. I think they were asking because they couldn’t believe that they were actually being asked to solve a problem that might not have an answer, a problem the teacher had not attempted to solve. This was a new problem, a raw problem. Could they really have ownership of this problem?  Was I genuinely offering it to them with no strings attached?

“We got it!  We did it! It is possible”  I looked over and two of the girls had this in front of them:

I asked, “are you sure?”

“Yes.  Look at it.”

At this point, I expected to hear sighs of frustration.  I thought the other students would be angry that these two girls had found the solution and now the problem solving was over. I was wrong.  I looked around the room and noticed that everyone else was still working on the problem.   Some had looked over, interested in what the girls had found, and then went back to their work.

From the other side of the room, Jon said, “I think there is another way.”  In front of him, were the beginnings of a rectangle with different dimensions than the one the girls had just completed.

“I just can’t figure out how to get rid of the tail, but I am almost positive it will work.”

The girls came over to watch them and said, “That won’t work because you have to use sixes and one of your sides is 14 squares long. 14 isn’t a multiple of six.”

Someone else came over. “I don’t think it has to be a multiple of 6 because one of your (the girls) sides is 46 and that isn’t a multiple of six.”

At this point, I thought about calling everyone together to discuss what we knew so far, but I decided against it.  There were only a few minutes left in the class and these kids were locked in – they were totally engaged in a beautifully raw math moment.  I couldn’t bring myself to take that away from them.

In a truly synchronistic way, the bell rang just as Jon declared, “I did it!”  He stepped back and let us all admire his work:

Nobody packed up.  Nobody ran out the door.  We all just stood there.

“There is an answer,” somebody said.

“Actually there are two,” someone else added.

Finally I asked, “I wonder if there are any other ways to do it?”

“Mrs. Caban, will you leave the graph paper pieces with us so we can see if there are any other ways?”

“Absolutely.  Keep me posted.”

As I re-read this blog post, I realize that I started the blog with a dangerous assumption.  I said, “Clearly my purpose was not to miraculously, in sixty minutes or less,  get these students to love math and see themselves as vital contributors in a math community.”

Wow.  If that isn’t my purpose than what is? I realize now that my purpose is most definitely to spend each second of those sixty minutes getting students to love math and to see themselves as vital contributors in a math community.   Who am I to think that anything less than that is possible?

ADDENDUM:

Thank you Tracy Zager for asking about the Math!  It prompted me to double check the arrays in the picture.  I think they are askew!  We left this lesson in such a rush that we never double checked the size and number of the smaller arrays inside the big array. Fortunately, I took pictures. Look what I found:

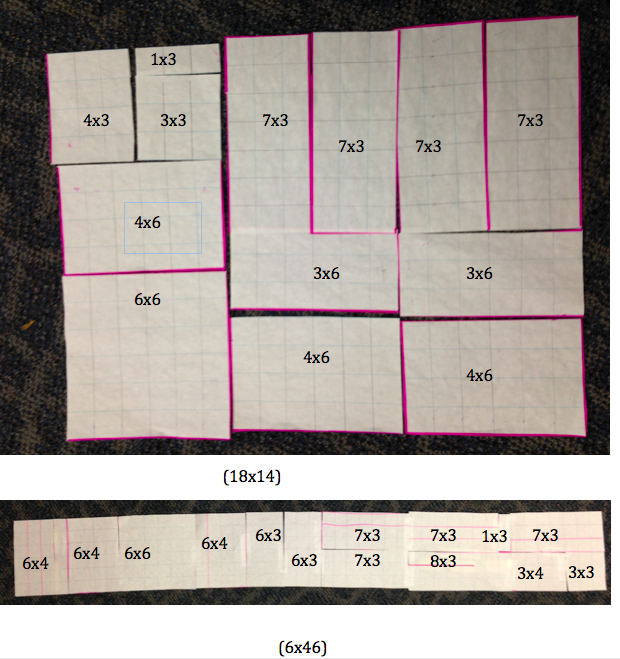
See comment below for reflections about whether or not to beat myself up about missing the opportunity to discuss this major difference with my middle school math buddies.