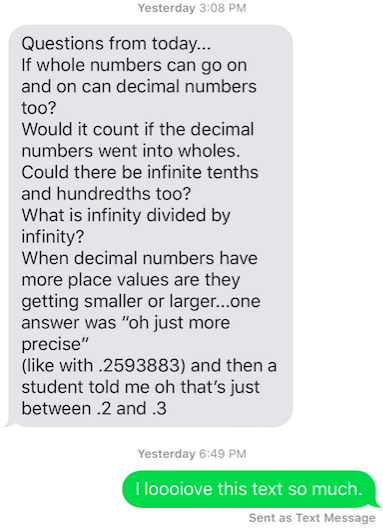
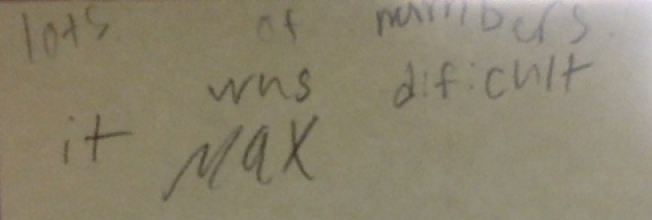Yesterday, after I taught math in Kindergarten, I went into my colleague’s office and cried. I didn’t see it coming. I was not prepared for it. Once I started, I had a hard time stopping. My friend Deb came in and asked, “what is wrong?”

“I still carry shame about learning, school and Math.”

“What happened?”

I told Deb. “It just sneaks up on me. I think I am over all that shame baggage, and then it comes back. I have just been thinking a lot about “those kids” lately. This past week I have worked with so many kids who hate math or think they are stupid.  Kids who don’t fit into “the mold” for one of a million reasons; because they don’t think like we want them to, they don’t learn fast enough, they don’t learn in a straight line, and maybe they can’t remember things or they mix things up.

“I am those kids!” I started crying again. “I was an English Major. I hated math. I was miserable at it. It was my worst nightmare. I got the message that I was not smart.  But, here I am! I am a district math coach! That’s great, right? I moved past it. I am in love with math. I am okay with confusion. I am drawn to things I don’t understand. I can be a role model, right? But still, deep down, sometimes, there is that little voice that wonders, ‘what if I’m not good at math? I know. There is no ‘good at math’. I know that. My rational brain tells me that ‘good at math’ is a farce, but sometimes, I just let that self-doubt creep in.

Last week I was in a high school math class. I asked the kids to tell me some words that described how they felt about math. They told me, ‘it is hell’ and ‘it sucks’. Some kids actually said things that were positive which was awesome.  One girl told me math was fun if she was baking. But another girl told me it was loathsome.  When I asked her to think of a word that described how she wanted math to be, she said, ‘tolerable’. That is it. That is all she wants; for math to be tolerable.

I told her, ‘I want to show you that Math can be inspiring.’

She said, ‘numbers don’t inspire me.’

I asked, ‘what inspires you?’

She said, ‘poems’.

I told her I was going to challenge myself this year to help her find math inspiring.

Then, last week, when I was in 5th grade, you know the blog post I wrote? Those boys have confessed to hating math in their lives.  They have told me more than once that they can’t do it. Those boys are amazing thinkers! Seth’s mom texted me after that math class and told me he talked about math the entire ride home!

Max, the other boy, asked Mrs. G and I , ‘why can’t math class be like this all the time?’ We said, ‘it can! You just need to keep asking questions.’ That is awesome, right! I should be happy about that. I am happy. I just had a hard time this weekend, while I was doing the math. Those boys inspired me. They inspired my friends on Twitter. We spent all weekend trying to solve problems about repeating decimals. I kept thinking about Seth and Max and their questions. At one point, I couldn’t tell where my thinking stopped and Max’s began. But, I made some mistakes. The people I was working with seemed to ‘get it’ a lot faster than me. I asked questions, that afterwards, seemed obvious.

(WARNING: UNFINISHED THINKING BELOW)

 

I am not sure what happened, but I started to doubt myself, somewhere in the middle of all those decimals.

After we taught Kindergarten, I came in here, composed a tweet, and started to cry.”

I think at this point, Deb said really nice things about me.

I know those nice things are true.  I know I am good at my job. I am pretty sure I inspire people to think differently about how they teach and learn math. Maybe it is not a bad thing that I am so sensitive to feelings of inadequacy.  Sometimes, I think it would be better if I could block them out, but maybe it is okay to let them in. I just need to remember:

-Becoming the Math Teacher You Wish You’d Had by Tracy Johnston Zager

So, I need to share one more story with you. Remember the Kindergarten class that I mentioned above?  Deb, Katie, and I have been meeting monthly to plan and teach a lesson together.

We are trying to learn more about how kindergarteners learn to record their thinking. Today, we decided to introduce a body sized ten frame. ( I forgot to take a picture of it before I left it with the kindergarteners so here is a picture from last year:)

These kids haven’t done a ton of work with ten frames, yet, so it was really interesting to hear what they noticed:

• It is pink and blue
• I notice squares.
• I see lines.
• I see rectangles.
• It looks like a window.
• The whole thing is a square cuz the long lines and short lines and long line and short lines.
• No, it is a rectangle because this side is 1,2,3,4,5,6,7 seconds (starts crawling around the perimeter of the ten frame) and this side is 1,2,3,4,5,6 seconds, then this side is 1,2,3,4,5,6,7 seconds again and this side is 1,2,3,4,5,6 seconds. Because one way is shorter and one way is longer.
• He noticed it is a square and there is one long second and one short second.
• You could put Xs inside the boxes.
• Yeah, you could put X, X, X, X, X, X, X, X, X, X
• You could do jumping jacks on them.
• I notice it is the yellow brick road because I was the Wizard of Oz for Halloween.

And here is what they wondered:

• I wonder if you could put them together to make a circle.
• I wonder if you could make the pink or blue a different color.
• I just noticed that there is ten squares of pink.

Listen to what happened next:

When I listened to the whole recording, I  heard a boy in the background saying, “1,2,3,4,5… 1,2,3,4,5”

I will call him Colin. Remember him.

After we introduced the body sized ten frame, we handed out collections of shapes. All of the collections were less than twenty.  We invited the students to use paper plates, cups, or ten frames to help them organize their count, if they wanted to.  We also gave each of them a recording sheet. Then, they went to work.

As I was circulating and chatting with students, I came upon Evan.  Evan’s shapes were scattered across the table. His recording sheet was on the floor and he didn’t have any organizational tools. I asked him, how many shapes do you have?

He said, “I don’t know. I can’t do this. I don’t know how to count.”

I said, “I think you can do this. I wonder if one of the organizational tools would help you.” I invited him to visit the table and see if any of the tools interested him.

He came back with a paper that had three ten frames printed on it. He sat down and began to put one shape in each of the squares. When he finished, he looked up at me and smiled:

I asked him, “how many shapes do you have?”

He gestured with his hand, sweeping it down the entirety of the full ten frame and said, “one full rug”. Then, he quickly waved his hand over the rest of the shapes and said, “and one half a rug.”

I smiled. I couldn’t help it. I am miserable at maintaining a poker face. I said, “You do, don’t you! You have one full rug and one half of a rug.”  At this point, I got the attention of the other friends at the table. I asked Evan if he would share what he discovered. Then, I asked Evan’s friends, “what do you think? Does Evan have one full rug and one half of a rug?”

They said, “Yes! He does.”

Then, I asked Evan, “how many shapes is that?”

He counted sixteen because he forgot the number thirteen.

I said, “I think you might have forgotten the number 13. Let’s count together and see what we get.”

We counted together, Evan smiling the whole time, and got 15.

“So,” I said, “When someone asks you how many shapes you have, you can say 15 or you can say one full rug and one half of a rug. That is pretty cool. Do you mind sharing that with the whole class when we come back to the circle?”

Evan beamed. He didn’t mind at all.

I walked away and was about to call everyone back together. Then, I spotted Colin’s paper:

I asked Colin, “how many shapes do you have?”

He tried to count them, but he got 24.  He counted to 11, but then continued with 20, 21, 22, 23, 24.

I asked Colin to look at Ethan’s shapes and tell me what he noticed.

He said, “We have the same amount!”

I asked Ethan, “How many shapes do you have?”

He said, “one full rug and one half a rug.”

Colin said, “Yeah! I have that too!” He gestured with his hands, just like Ethan did and said, “one full rug and one half a rug”.

I asked Colin if he would mind sharing what he noticed during our closing circle.

Originally, I thought I was going to facilitate the closing circle to highlight the ten structure. Ethan and Colin threw me a curve ball. They were thinking differently. They were thinking about one whole. I changed my plan. I drew models of Ethan and Colin’s ten frames on the board. I asked Ethan to tell us what he found out. He said, “I have one whole rug and one half of a rug.” Then, I asked him, “how many shapes is that?” He counted 15. I wrote it under his ten frame.

Next, I asked Colin to share what he learned. He said, “I had one rug and a half a rug.”

I wondered, “How many shapes is that?”

He counted, “1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 21, 22, 23, 24”

I said, “you told me that you and Ethan had the same amount of shapes. It looks like you got different amounts. What do you think about that?”

“We do,” he said, “one whole rug and a half of rug.”

“Yes! I see that. You both filled in one rug and one half of a rug. Ethan says that is the same as fifteen shapes. You counted 24 shapes. Can we count your shapes again?  We can count together.”

I wrote the numbers 13, 14, and 15 next to three of the dots. I am not sure if this was the correct thing to do because I might have further confused the matter by assigning a dot a number name, but I was trying to give him a visual reminder.

I said, “Let’s count together.  We choral counted to 15.”

Then, he said, “I only need five more! I only need five more until I get to….” He started counting again from the beginning. “I only need 5 more until I have 24!”

At this point, Katie asked the students, “how many shapes do I have if I fill one of the rugs?”

Some of the students started counting. Some of the students were spinning around. One student was very busy trying to convince Colin that he counted wrong. It was 1:30 on the Wednesday before Thanksgiving vacation. They were done. However, right before we pulled them back together to close up, one little friend said, “ten”. “There are ten shapes in a whole rug.”

I thanked Ethan and Colin for sharing what they discovered. I said “we learned that there are ten boxes in each rug and that the rug can help us organize our counting.  We also learned that there are different ways to count. Many of us were counting each shape, one at a time, but Ethan and Colin showed us that we can also count by the number of rugs we fill. We learned that 15 shapes fill up one rug and one half of a rug.”

On my way out, Katie approached me. She said, “Thank you. Thank you for highlighting Colin and Ethan. They really struggle with counting. They felt so good about themselves today. I am so glad that I got to see what you saw. They counted!”

 

 

Yesterday, I got this text:

It was from Mrs. G, the teacher I worked with on Tuesday.  I really wanted to check in with these kiddos and talk with them about these questions.  Today, I stopped by to ask them to tell me more.

First, I checked in with Ms. G. She told me that these questions came about when the class was doing a choral count.  She said the class was counting by hundredths. When they got to nine hundredths, someone suggested the next number might be one whole. Then, the students had a conversation about how it wouldn’t be one whole. It would be ten hundredths or one tenth.  They continued counting until sixteen hundredths. At this point, Max said, “wait! When we are doing this, are the numbers getting smaller or larger?” This question prompted a different question from Seth, “If whole number places can go on and on forever, can decimal places too?”

At this point, Ms. G wrote a long decimal up on the board and asked, “can I do that?”  Charles said, “I think that number would still be between 2 tenths and 3 tenths.”

Max responded, “wait! Can you just keep putting places because once you get ten of them, it is going to go into the next place and once you get ten more it will go into the next place and on and on.”

After Mrs. G caught me up, I turned my attention to the kids. I asked them if we could talk about this number again.

Max immediately jumped in to the conversations. He said, “yesterday, Seth asked if decimals go on forever and I was the only one who said, ‘no.’ I don’t think they would go on forever because eventually they would all add up to one.”

I wasn’t sure if I understood what Max was saying so I asked him to explain it. Listen.

 

“That is why I don’t think that you could count forever in decimals because I think eventually this will add up to one like I did here. I think that wouldn’t work. Eventually, no matter how big the number is, if you’re still adding, eventually, even if it takes years, it will eventually make one whole.”

At this point, the students went back to their Social Studies lesson. Yes, it is true. I totally interrupted Social Studies to revive a math lesson. I love Social Studies, but sometimes, I think it is okay to Drop Everything and Do Math.

Mrs. G and I went over to the kidney shaped table to reflect a little. Mrs. G took some time to share the back story of these questions. She explained what happened the day before. Listen.

I wondered, what is Max’s claim?  Is he claiming that decimal numbers DON’T go on forever or is he claiming that all unit decimals (is this a thing?) will eventually add up to one whole? Mrs. G and I wondered how language was impacting our conversations with Max.

Mrs. G said, “I think I kept saying “adding” a place value.  Can we keep “adding decimal place values”? Max is hearing the word ‘adding’. Maybe he is thinking about counting as adding.  We decided to ask Max a few more questions about his claim, but try to use more precise language this time.

When Max sat down, I said, “I want to try to understand the question you are asking.”

He said, “Well. I only half understand it myself.”  Have I mentioned, yet, how much I absolutely love this kid?

I tried to rephrase Max’s claim without using the word ‘adding’. Listen to the conversations:

I have listened to this clip several times and I wish I had done something differently. When Max says, “so you are just adding place values. You are not adding the numbers one by one.”, I wish I had not said anything. I wish I would have waited and let the magnitude of his statement settle into the silence. 

Max goes on to rephrase his claim. He says, “no matter how small the number is, you are eventually going to get to one whole, no matter how long the number is, even if you give up, if you didn’t give up, eventually it will go back to one whole.”  

Now that I think I understand Max’s claim, I am wondering how it fits in with Seth’s original question about whether or not decimals can go on forever.  Listen as Max invites Seth into our conversation:

So, at this point, I am still wondering about what Max is disagreeing with. When he is talking to Seth, he says, “And I asked, without it going into wholes? Did you mean adding?” These words make me wonder if Max is still talking about the cumulative addition of unit decimals, as opposed to the literal writing or naming of a decimal number.

I told Max that I was still unsure. As we talked, I wrote the number below. Listen.

Next, Max catches me off guard. He is thinking so fast, I have a hard time keeping up with him.  I was trying to see if we all agreed that I could keep writing digits forever. However, I got lazy and just started writing zeros. Well, that added a whole new layer to the conversation.  Max didn’t miss a beat. Listen.

This kid is thinking so fast and so deep that I can’t keep up.  I started using the word “adding” again which didn’t help with clarity.  Fortunately, Max persevered and straightened me out, at least as far as the whole “zeros question” goes.

I was still unsure about whether he thought decimals could go on forever. He keeps bringing in these other nuanced constraints: “without it going into a whole”, and “you have to count with decimals by one.”

I asked him, “what if I didn’t write zeros. Couldn’t I just keep writing digits forever?”

He said, “That is not correct. You’ve got to do one and then another plus one to make a zero. You can’t just add ten numbers at a time or seven numbers at a time.”

At this point, I tried to sift through what I thought were two different claims- one about writing/naming decimals and one about counting/adding decimals. Listen:

I am not totally sure we all ended up on the same page about understanding our claims, but this conversation with Seth and Max was one of the highlights of my career.  I could probably spend the rest of my day just reflecting on this conversation.  These boys pushed me to think differently and to try to truly understand them. What if we all did more of this?  What if we dropped everything and did math? What if we dropped everything and listened to understand each other’s thinking?  I am so grateful for these boys and their amazing thoughts. I tried to conclude our conversation by letting them know how much I appreciate them. Listen

 

Recently, I read a blog post by Andrew Gael, Our kids Are Not Swiss Cheese.  Some quotes that stuck with me from Andrew’s blog:

• “Maybe it is not the learners; maybe it is the way that we conceptualize learning…”
• “Learning is complex, multi-leveled, and no one is all the way “filled in.””
• From Megan Franke, “How do we notice and use what students DO know to support them to make progress in their thinking?”

Last week, during our 5th grade collaborative planning session, we discussed how to introduce decimals to our students. We decided we wanted to start by unearthing what the students already understood about decimals.  I was really excited to approach “decimals” as a concept that connects to prior knowledge, instead of a series of disjointed procedures.

So, today, we started our journey. I co-taught with Mrs. G. and Abby, our school based math specialist, co-taught with Mrs. C.  We wrote this question on the board, “What are decimals?”  We told the students we would ask them for their thoughts about this question at the end of class. Then, we counted.

We started counting by ones and tens. Then, we asked them to count by tenths.  That is all we said, “let’s count by tenths. Who wants to start?”  Matt said he wanted to start.

“one tenth.”

I asked, “how would you like Mrs. G to record that?”

“Just write one tenth.”

“Can you tell us what that will look like?”

He went over to the white board and wrote this:

“Okay,” I said. Mrs. G recorded ‘one tenth’ on our chart.  Then, I asked Gary to continue the count.  We continued the count, each time asking the student how they would like us to record what they said.  This is what they told us:

If someone was unsure, we told them we could put a question mark above their suggestion and we could come back to it.  It was so interesting to me how quickly the students began referring to each other as authors of ideas. When asked, “how would you like us to record that?”  They said, “like _______ did.”  When we got to nine tenths, one student told us he would like us to record it ‘the same as six tenths, but with the slash the other way.’  I actually have a voice clip.  Listen.

 

As I listen to this clip now, I am smiling. I love it. I hear confidence and creativity. The first time I heard it, I was nervous. I wondered, should we put that on the chart?  What if the students think it is an acceptable way to write a decimal?  What if I ruin them forever by supporting this backwards slash business?  I almost panicked. There were so many times during this routine that I almost caved. I almost said, “actually, that is not how we write decimals.” But, I didn’t. I am so glad that I didn’t.  Look at this chart! I mean really look at it.  What do you notice?  What do you wonder?  What do these students know about decimals?  What do these students know about our number system?

Yes. There are definitely some partially formed ideas here. There is no doubt that we need to continue our study of decimals.  Of course we do. It is only day one.

After we finished our count, we told the students that we will continue to look at this anchor chart and we will continue to count by tenths. We also asked them to write down something they noticed and wondered about our chart.

We asked a few kids to share their thinking: B shared his thoughts about 2.5 = 2.50, S shared his question about whether we can write decimals in word form and we confirmed that we can, K asked about writing decimals in exponential form and we told him it is possible, but we would talk about that in more detail later. At the time of the lesson, Mrs. G and I were so bummed that no one noticed the ten in a row pattern. As I write this blog, I realize Molly DID notice it. Arghh!  We will have to ask her to explain her thinking tomorrow.  Maybe we can compare and connect Molly’s, Patrick’s,  and Gabe’s responses.

Next, we split the kids into two small groups.  Mrs. G took half and I took half. When we made our heterogeneous groups, we considered processing time, distractibility, schema, perseverance, expressive and receptive language, etc. We spent less then 5 minutes, but we considered all of these criteria as we tried to form groups that amplified the learning experience.

Mrs. Gordon and I each facilitated a Number Talk using the following images:

This slideshow requires JavaScript.

My group had some really interesting conversations.  I was worried that, if we used money, it might limit our conversation to one context, but I don’t think it did. One of the most interesting questions they asked was when they wondered whether 1.50 and $1.50 were the same or different. What a deceptively simple thing to wonder about. This next clip is really interesting.  I like it beacause I think it is an example of what Andrew discussed in his blog. Can you hear the non-linear complexity of ideas being formed?

 

To close out the lesson, we asked the students to do two things. First, we asked them to answer the question, “what are decimals?”

We also gave them a question to think about.  We asked them to tell us whether they thought the statement was true or false and explain why. We didn’t expect them to get the answer *correct*.  In fact, we were less interested in correctness and more interested in how they explained what they understood so far. Here is what they came up with:

After the lesson, Abby and Mrs. C check in while Mrs. G brought the kids down to lunch. Then, Abby told me how it went  in the other 5th grade class. Then Mrs. G and I checked in while Abby went to lunch. We were all wondering what to do next. We decided we would continue with the plan we had sketched out last Thursday. Tomorrow, we will introduce the kids to the Zoom in on the Number Line routine. We will try to connect the magnitude of tenths and hundredths as we compare decimals and place them on number lines with varying intervals. We also decided we would re-use our artifacts from the lesson close.  We are going to give the exit ticket and sticky note answers back to the students throughout the week and ask them what they would add and/or change.

Finally, on my way to Wayne Elementary School, I stopped at varying spots to collect artifacts that reminded me about decimals.  Here is what I came up with.

I texted my artifacts to Mrs. G and Mrs. C and asked them to ask the kids to go on their own scavenger hunt for decimal related pictures or conversations that they wonder about.

I got my first response:

So, yeah, it is scary to invite kids to put a bunch of partially formed ideas on the table. It is messy and it will take us awhile to sift through them and make connections, but I think it will be time well spent.

Last week, I was reading Tracy Zager’s book, Becoming the Math Teacher You Wish  You’d Had.  I tweeted her to let her know that it was going to take me years to finish her book because it so rich with provocative ideas.  Here is one that I have been mulling over for days now:

“Above all else, maintain your focus on developing young mathematicians who listen to and refine their internal truth detectors. Encourage them to be skeptical and allow them to remain in doubt until they are genuinely convinced. Do not apply pressure to concede, even, if you’d like to move on.”

I just love that. I would be pretty psyched if, some day, some thirty-something mathematicians tracked me down to thank me for helping them refine their internal truth detectors.  Thanks again for the push Tracy.

Last weekend, I wrote about my experience doing Number Talks in two high school classrooms. I got some really helpful feedback.

After I read the blog post Pam recommended, I read the pages from her book that were referenced in the blog post. Then, I started to plan the string I would use in the Transitions to Algebra class. I thought about, why would I use the string Pam recommended?  How does that string fit with what we are trying to do with our students?

Then, I anticipated what our students would do and say when I presented the first problem in the string:

So, that is how I planned to introduce the string. Here is how it actually went down:

When I walked into the classroom, Ms. S wasn’t there. The bell hadn’t rung yet. All nine students were scattered around the room. Some were sitting in pairs and others sat by themselves. I told the students how glad I was to be back.  As I connected the Smartboard, to my computer, I chatted with the students. I checked in with each of them to see if I remembered their names correctly.  A group of girls tested me.

I asked their friend, “I can’t remember, is your name Megan or Meegan?”

They laughed and said, “Megan”.

Someone said, “no. Her name is Meegan.”

More laughter.

At this point, Ms. S came back in the room. As soon as she sat down across from Riley,  he looked at her and said, “I hate math. I just hate it.” Ms. S reminded Riley how hard he had been working and how much he is learning this year.

I asked her, “Is it Megan or Meegan?”

She said ,”Meegan.”

“Thanks.”  Then, I officially started my lesson.  “So, last time I was here we were doing some multiplication. Today, I planned a Number Talk that is a little different. Today’s Number Talk problems are going to be about a situation. We are going to talk about bags of m&ms.  Not the big bags. The little ones.”

Ms. S chimed in, “The fun size bags.”

“I have one of those!” Hayley said, as she dug into her sweatshirt pocket. She held up a little red bag. “Forget it. These are Skittles.”

Several students erupted, “Let’s do Skittles. I hate m&ms. Skittles are so much better than m&ms.”

“Not today,” I said, “maybe next time we will talk about Skittles. I am so glad Hayley had a bag of Skittles in her pocket because the m&m bags look a lot like the Skittles bag. Now we all have a clear idea of the size of the bags. Thanks for adding to our context, Hayley.”

“Okay. So , today, I want you to consider bags of m&ms. Each bag of m&ms has 17 m&ms in it.” I wrote in the table as I spoke:

“Think about how many m&ms would be in 2 bags. Please don’t say your answer out loud. You don’t have to raise your hand. Remember, you can show me a thumb when you have a possible solution.”

Some of the kids held thumbs in front of their chest. A few kids raised their hands.  Meegan blurted out, “like 30.”

I said, “So Megan…”

Laughter. I looked at Ms. S and she said, with a smile, “it’s Meegan.”

I smiled, “See what happens when you mess with me? I have trouble remembering names when I hear them correctly the first time.”  I continued, “So Meegan, can you use your thumb next time. I totally appreciate that you are participating, but I want to make sure everyone in the room gets enough think time.” I wrote her solution on the smart board.

“Are there any other solutions?”

“30 something.”

I was about to ask Riley why he said 30 something, but Max started talking, “34 because 10 plus 10 is twenty and 7 plus 7 is 14 and 20 plus 14 is 34.” As Max was talking, I started recording what he was saying:

In the middle of Max’s explanation, Riley started a monologue of verbal processing, “No. I did 20 plus 7 is twenty-seven, but now I have to add seven more and I lost count. You need to add the 7 to the twenty….”

I need you to picture those conversations happening simultaneously, while Meegan is having a side conversation with Katie and drawing on her hand. I wish I had an audio of it.

The two boys were talking at the same time. They weren’t trying to be difficult. They weren’t intentionally ignoring each other. They were just being impulsive. My greatest struggle with this class is that they are incredibly impulsive. If you know me at all, you can feel free to chuckle right now. I get it. The impulsive leading the impulsed.

“Okay,” I said, “hold on. I really want to hear all of you and I want you to hear each other.” At this point, Ms. S went over to Meegan and asked her to put the marker away.  I continued, “Max was telling me that he thinks the answer is 34 because he added 17 plus 17 by decomposing the 17s. Max, did I record your thinking correctly?

“yes.”

“Okay. Riley, it sounds like you did not solve the problem that way. Am I correct?”

“Hold on,” Riley said, “Ten plus ten is twenty and then plus seven is twenty-seven. Now, I have to add 27 plus 7. Ugh. That is the worst.  27, 28, 29, 30, 31, 32, 33, 34. Okay, yeah, 34.”

I tried to record his thinking:

I asked, “Does my recording represent what you were thinking?”

“yes.”

“Okay. So, we just spent a lot of time talking about addition. Can anyone see a multiplication problem in this situation that we are talking about?”

Matt said, “17 x 2”

Riley asked, “Is that the same as 2 x 17?”

“Yes!” Said Ms. S. Later, Ms. S told me that Riley has been thinking about the commutative property a lot lately.

“Okay,” I said,  “so we can say that 17 + 17 = 17 x 2?”

“yes,” they agreed.

Next, I asked, “What if there are 4 bags of m&ms?”

Olympia blurted out, “41”.

I recorded it and reminded her to please show me a thumb.

I think she said, “sorry.”

I saw a few thumbs and a few raised hands.  Several students, to include Samantha, had yet to participate. I asked Porter, “Do you have a solution? You can pass if you want, but I would love to hear what you are thinking.”

“pass.”

“Hayley, do want to share a solution?”

“pass.”

Riley said, “I got 68.”

Hayley said, “me too.”

Olympia said, “I got 41. It’s wrong.”

Riley added, “I think you only added one 17.”

Max and Matt were having a side conversation about why the answer wasn’t 41. Meegan and Katie were giggling about something that I am pretty sure had nothing to do with math. I was trying desperately to NOT lose the exchange that just happened between Olypia and Riley.

“Riley, are you saying that you think Olympia got 41 because she only added one bag of m&ms, instead of two?”

“Yeah. She only added one 17. She needs to add another one.”

“Okay! So we can add that to our table. Where can I put that?”

“you can put a 3 in between the 2 and 4.”

I did.

So… I did NOT anticipate this conversation happening. That might be why I didn’t actually notice that 34 plus 17 is NOT 41. It is 51.  I was so excited that Riley was thinking about Olympia’s mistake in the context of the problem that I didn’t even catch the arithmetic mistake.

Keep in mind, Meegan is still having a side conversation. Samantha is drawing on her whiteboard (where did she get a marker?).  Max and Matt are explaining their solutions to each other, completely ignoring the rest of us. Oh…. and Bill, Hayley, and Porter haven’t said a word in a long time.

“Can everybody listen for a second?” I asked. “I absolutely love coming into this class to do Number Talks with you. It is the highlight of my week. I learn so much from you, but I get really frustrated when you are all talking at once. I want you to be able to hear each other. Can we please try to take turns when we talk?”

It got quieter.  It was not totally silent, but everyone was making eye contact with me and attempting to pay more attention then they were before I started speaking. I’ll take it.

At this point, I asked, “where is the multiplication in the work we are doing?”

Matt mentioned doubling again. I asked him to show me where the multiplication was, in regards to doubling.

He explained, “17 x 2 is 34 and 34 x2 is 68.”

We continued to discuss the amount of m&ms in eight packs.

 

Then, I asked about ten packs. Several students said, “170.”

Riley said, “one hundred something.”

I asked, “how do you know it is one hundred something?”

He explained, “well ten times ten is 100, but then I have to add ten sevens and I can’t do that in my head.”

Matt said “dude, you don’t have to do that. There is a much easier way. Whenever you have something times ten you just add a zero to the number. Seventeen times ten is seventeen plus a zero. It is 170. You are making it harder than it needs to be.”

I said, “okay, can we slow down a second? What Riley is saying and what Matt is saying actually go together. Matt is talking about the procedure and Riley is talking about why the procedure works.  Riley, can you repeat what you started to say?”

As he spoke, I drew an area model on the board.

Halfway through my drawing, Matt spoke up again, “you don’t have to do all that. You just add a zero. You are making it harder than it needs to be.” Matt is not trying to be disrespectful.  Matt is trying to help his classmate.

I said, “Matt, you are trying to show Riley a trick that helps you. Riley is trying to understand where the answer is coming from. I think Riley’s strategy is connected to what you are saying.”

Riley said, “I just don’t know 7 times 10.”

Meegan said, “it is 70. You just add a zero.”

Riley agreed, “Oh yeah! Okay. Yeah. The answer is 170.”

At this point, I REALLY wanted to revisit the commutative property with Riley, but there was so much else to consider. Matt was getting frustrated that we were spending so much time discussing a strategy that, in his mind, was needlessly cumbersome. He wasn’t frustrated with his classmates. He was trying to help them. He was frustrated with me.  He didn’t understand why I was “wasting” all this class time talking about something that had no relevance to him.  Why didn’t I just tell Riley to “add a zero” and move on with the Number Talk?  So, for better or worse, I moved on.

“Okay, let’s talk about 12 packs. Ms. S, can you give everyone a marker? I would like all of you to record a solution on your whiteboard. Try not to use the whiteboard to solve the problem, but use it to record your solution. I want everyone to at least try, please. You can write your answer really small, if you want. I just want to see something so I know that you tried.”

Right away, Meegan wrote 204 and then covered it.  She looked up at me and whispered, “Do I have to keep it uncovered?”

I said, “I saw it. You can keep it covered it, if you want. Just don’t erase it.”

Hayley wrote twelve seventeens on her whiteboard and started to add them. Olympia had three hundred something written on her whiteboard. I can’t remember the exact number. I waited about 2 minutes.  Hayley was still adding twelves. Bill hadn’t written anything but had that “mental math” look on his face (eyes looking at the ceiling, lips moving, head nodding in sync with a count,).  Matt was describing to Max how he added 34 to 170. Meegan, Olympia, Samantha, and Kate were doodling.

“Okay,” I said, “you might not have a solution yet and that is okay. I want us to start a conversation about what we think so far. Meegan, can you tell us where you got 204?”

“I added 34 and 170.”

“Can you tell us why you did that?”

“Because that is 12.”

“What is 12?”

“204.”

“Twelve what?”

Meegan responded, starting to get frustrated, “you asked how many are going to be in twelve!”

“Right. I did. Okay. So you added the amount of m&ms in ten bags to the amount of m&ms in two bags?”

“yes.”

At this point, there was a lot of agreement about Meegan’s answer. Everyone thought it made sense.

“Okay,” I said,  “Does anyone see a multiplication problem in the problem we just solved?”

For the next five minutes, we engaged in a round of Guess What the Teacher is Thinking. I hate this game and I try so hard not to end up playing it, but sometimes, I get caught off guard. The kids were not really sure what I was asking.  I should have just said, “You told me that 2 bags of m&ms was 2×17 and ten bags of m&ms was 10×17. So…..”  But I didn’t say that. I actually don’t remember what I said. I just remember the distint feeling that the kids were trying to guess what I wanted them to say.

I am not sure where it came from, but, eventually, Riley said,  “so, do you mean twelve times what is 204?” I wrote it on the board.

“Let’s go with that. So, what did we multiply 12 by to get 204?”

This is where the lesson got really interesting. No one saw the 17. Meegan mentioned that she added 34 and 170. Matt and Max were discussing how they added 170 and 34.

I asked Hayley, “Do you mind sharing what was on your whiteboard before you erased it?”

She smiled and said, “It was so stupid. I am so stupid.”

I said, “I don’t think it was stupid. I don’t think you are stupid. In fact, I think it is going to really help us answer this question. Right now, we have an answer that we know makes sense, but we are struggling to figure out how to write the problem using multiplication. I think what you had written on your white board will help us. You can pass, but I would love it if you shared your work with us.”

She said, “pass.”

“Do you mind if I talk about what was on your white board?”

“That’s fine,” she agreed.

I said, “Hayley had the number 17 written on her white board 12 times,”

Riley interupted me, “It is 17! Of course it is 17. It is 12 x 17!”

“Yes,” I said. “It is 12 x 17. Hayley, your work was really important because you were the only one who thought about the problem as 12 groups of 17.  We needed to hear about your work to remember that we are multiplying 12 x 17.”

Then, I asked, “Where is 12 x 17 in Meegan’s solution? Meegan said that she added 34 and 170. Where is 12 x 17 in her work?”

Matt said, “Well 10 plus 2 is 12 so there is the 12.”

I asked, “where is the seventeen?”

Somebody responded, “There is a 17 under the one, but that isn’t the seventeen that Meegan used.”

We had been Number Talk-ing for awhile.  I decided to wrap it up. I drew another area model of 17×12. I explained that Meegan’s strategy works because of  the distributive property. Our table showed 10 bags of 17 (or 10×17) and it also showed 2 bags of 17 (or 2×17).  Meegan added the partial products to find out how many m&ms would be in 12 bags of m&ms.

I added that Riley was using the distributive property earlier when he decomposed 17 into 10+7.

Riley erupted, “can we call that ‘Riley’s Law’?”

“Sure,” I said. “It is also called the distributive property, but Riley’s Law works for me.” I wrote Riley’s Law next to the area models.

After class, I chatted with Robyn, the high school Math Specialist who has been collaborating with Ms. S. Robyn was in the math office and I asked if she had a minute to reflect with me.  I described how our class went. I asked her to help me think about what we might do next time.  Here are the notes I took:

After I chatted with Robyn, Ms. S came into the office. We started chatting.

She said, “I am sorry they were rude to you. I talked to them after you left. I have been wanting to revisit our classroom expectations. I told them if they acted like that next time, there would be consequences.”

I said, “We should also revisit our Number Talk expectations. How about next time we create an anchor chart that defines the purpose of the Number Talks and the expectations. We did that in September, but we didn’t write it down anywhere. Also, now that we have done several Nubmer Talks together, the conversation about norms and expectations will have more meaning.”

“I like that idea,” said Ms. S. “Can you lead that conversation?  I would really like to see what it looks like. I will support, but I would love to watch you do it.”

“Sure,”  I said.  I took some notes as we processed the different behaviors we saw today and how they impacted our learning.

Then, I shared the conversation that Robyn and I had about the content of our next Number Talk. Ms. S agreed that the plan Robyn and I came up with would be a good next step. We both had to run to a meeting, but I am going to ask her if we can set up a time next week to anticipate student responses and create a monitoring sheet. Maybe Robyn can join us.

My favorite moments are when frenetic, seemingly unrelated experiences lead to serendipitous learning.  This week, I engaged in several different reflective conversations on Twitter. One was about my high school Number Talks experience. Another was about teacher collaboration, and the third was about a little boy’s response during a Which One Doesn’t Belong routine.  In my non-virtual life, I was reading chapter 11 of Tracy Zager’s book Becoming the Math Teacher You Wish You’d Had and facilitating several really hard conversations about why collaborative interventions are best for kids.

I wonder, how do I stay intentional when real life veers from my plan?  I think, after writing this really long blog, the answer lies in honing my intuition. There are a million things I could have done differently during the Number Talk that I just described. Okay, maybe not a million, but I have thought of at least five just while I was writing this blog.

My best attempts at reflection usually involve finding a crossroad in the journey, revisiting the path I took, and exploring the path I might have taken. If the reflective process works, it leads me to a truer understanding of my intentions.

The most important teaching decisions are made in those micro seconds, when things don’t go as planned and we have to use our intuition to decide what to do next. My intention is to shine the light on those moments so we can all think about them together.  I try to write about the messy stuff: the moments of uncertainty, confusion, and frustration.  I try to write about the times when things didn’t go exactly as planned because, in my teaching and coaching experience, they never do.

 

As a K-12 math coach, I am all over the place.  We have about 50 teachers in our district who teach math in some form.  I haven’t found a way to divide my time equally among those 50 teachers and make a difference. My superintendent tells me to work with teachers who want to work with me.  So I do.

In the beginning of the year, I had two high school math teachers ask me if I would do Number Talks with their classes. I was thrilled. First, I gave them both a copy of the book, Making Number Talks Matter by Cathy Humphreys and Ruth Parker. (If you don’t have this book, go get it.) Then, I added both classes to my calendar and told them I would be there, once a week,  for the rest of the year.

I didn’t have a pre-planning meeting with them. I didn’t write down formal goals.  I probably could have. Should have? The reality is I don’t always make the time to follow elaborate coaching protocols. I am not saying that I shouldn’t. I probably should, but I don’t.  My number one priority is getting into a classroom, as quickly and regularly as I can.  My number two priority is getting invited back. All the formal protocols in the world aren’t (necessarily) going to help me build relationships, BUT building relationships might help me use coaching protocols more meaningfully.

Ms. S and Ms. K, were really excited about me doing Number Talks in Algebra II and Transitions to Algebra.  They talked about wanting to build their student’s number sense and get them to have more meaningful math conversations.  Those sounded like great goals to me. My unofficial goal for the first few Number Talks was to cultivate a space where the guiding principles for Number Talks could bubble up.  In chapter three of Making Number Talks Matter, Cathy and Ruth introduce ten guiding principles:

• All students have mathematical ideas worth listening to and our job as teachers is to help students learn to develop and express these ideas clearly.
• Through our questions, we seek to understand student’s thinking.
• We encourage students to explain their thinking conceptually rather than procedurally.
• Mistakes provide opportunities to look at ideas that might not otherwise be considered.
• While efficiency is a goal, we recognize that whether or not a strategy is efficient lies in the thinking and understanding of each individual learner.
• We seek to create a learning environment where all students feel safe sharing their mathematical ideas.
• One of our most important goals is to help students develop social and mathematical agency.
• Mathematical understandings develop over time.
• Confusion and struggle are natural, necessary, and even desirable parts of learning mathematics.

The first couple of Number Talks I did in both classes were kind of a hodgepodge. I was trying a bunch of things, looking for the “sweet spot” of just enough disequilibrium to prompt some spontaneous questions, revisions, and “wait… what?” moments.  I was less interested in the content of the Number Talk. I was cultivating the process. I started with dots and subtraction.

 

This slideshow requires JavaScript.

I saw all kinds of strategies from counting dots one at a time to subitizing.  Most kids said they used the algorithm for the subtraction problems. A few subtracted too many and adjusted. I thought one student used constant difference, but it turned it I was just projecting my thinking onto her strategy.  Many of the kids seemed to feel comfortable sharing their ideas.  Some were really open about changing their thinking.

The next time I came in, I used only dots and a Number Talk Image.  I wondered if the images would “nudge students beyond the algorithms.”

 

This slideshow requires JavaScript.

The highlight of this class was when I heard one student say, “I used ________’s method. I added dots in the corners, multiplied, and then subtracted the dots that I added.”  I hadn’t officially named the strategies. I hadn’t even “officially” encouraged them to try each other’s strategies.  They just thought “R’s strategy was cool.”

Cathy and Ruth talk about the importance of “helping students develop social and mathematical agency”.  They say,  “Students with a sense of agency recognize that they are an important part of an intellectual community in the classroom; that they have worthwhile ideas to contribute, and that they learn from considering, and building on, the ideas of others.”

For the next Number Talk, I decided to try some multiplication.  I know, I am all over the place.  Remember, I am just poking around right now.  I am trying to see what these students are willing to share, what they know, and what they are not sure of.

A lot of the strategies used during this Number Talk were based in addition and many students struggled to figure out why their partially correct approaches  were not working.  There was a whole lot of talk happening, which is why it went way beyond 15 minutes. It might have even lasted 30 minutes. Don’t call the Number Talk police, yet!  These kids – all of them – were so present and invested.

 

This slideshow requires JavaScript.

When it came time to discuss 35 x 24, they were talking over me and each other.

They were arguing.

There was one girl, who always sits outside of the group, by the wall. She hadn’t said anything in a while – maybe not ever.  I heard her whisper, “I don’t think you can do that.”

I barely heard her because two other students were going back and forth about whether you should multiply 35 x 2 or 35 x 20.

I had to raise my voice a little, ” Hold on! You need to be respectful of each other’s ideas.  I want to hear all your thoughts, but you need to be respectful and I can’t hear what _____ is saying.” They listened! I swear to you that they actually listened to me, and there is no doubt in my mind that the only reason they listened to me was because I said I couldn’t hear their classmate.

It was silent. I was super nervous, but I asked anyway, “Do you mind saying more? You don’t have to, but I would love to hear your thoughts.”

She said, “I am just not sure if you can do that. I don’t know the answer, but I am not sure you can just add the four like that.”

“Do you think we should multiply 35 by 20 or 2?”

“I think 20 because it is twenty four, but I don’t think we can add the 4 after that. It doesn’t seem right.”

“Yeah,” the boy said – the one who originally suggested an answer of 704 – “I don’t think it makes sense either, but I am not sure what else to do with it.”

It was silent. I thought about drawing an area model, but I just couldn’t bring myself to do it. I didn’t think it would mean anything to them. I am not saying I will never show them an area model, but I just couldn’t commit to it at that moment. Instead, I waited.

A different girl said, “I got 840, but I think it is wrong.”

I asked, “how did you get it?”

“I did it on my whiteboard. 4 times 5 is 20, carry the 2, 4 times 3 is twelve, plus 2 is 14, 2 times 5 is ten, carry the 1, 2 times 3 is 6 plus 1 is 7. 140 plus 70 is 840.”

I was kind of bummed. Where did she get a whiteboard? It must have been in her desk.

At this point, I remember feeling completely overwhelmed and exhilarated at the same time. How can I get them to see the groups of 35? I decided to show them what they already knew.  We went back over the other problems in the string.

“We know that 35 x 20 is 700. We talked about how multiplication can mean ‘groups of’. We can see the twenty groups of 35.  How many more groups of 35 do we need?”

Someone said, “I think we need to do 35 times 4, not just plus 4.”

I asked, “what do other people think?” I really wanted to scream, “YES! You are so right! We definitely need to multiply the 35 by 4!” I didn’t.

“I don’t know,” somebody said. “It seems like we could add the 4, but then it doesn’t.”

I was exhausted.  They were exhausted. I didn’t know what to do. Should I leave them hanging? Should I draw an area model?  Should I add 35 twenty-four times?

I think I wrote the partial products on the board and asked, “Why does this makes sense?”

I think at least one or two kids were able to articulate that we needed to multiply 35 times 4. I am pretty sure one of them referenced 35 x 20 being 700 so 35 x 24 had to more than 704.  There were definitely more than a few kids who were still unsure, but they looked like they would take our word for it.

One boy said, “that was so hard. My brain hurts.”

Silence.

“Can we do one more?”

I laughed. I said, “No. I want you to want me to come back. Everybody looks pretty fried right now.”

On my way out, I said, “I think multiplication is a good place for us to spend some time. Do you mind if I bring another multiplication string next time?”

They nodded. I think one of them even thanked me for coming. Their teacher, Ms. S, said, “that was so cool. I am learning so much from these Number Talks.  I didn’t learn how to do math like this when I was in school.”

I have read several books about math coaching and I have found them helpful.  However, my favorite way to think about math coaching is through the lens of a teacher.  Often, when I read books about teaching math, I replace the word “students” with “teachers” and I find provocative advice for myself:

“Teachers with a sense of agency recognize that they are an important part of an intellectual community in the classroom; that they have worthwhile ideas to contribute, and that they learn from considering, and building on, the ideas of others.”

So, at this point, I have done about four Number Talks in each high school math class. Tonight, I emailed Ms. S and Ms. K. I asked them,

• What have you noticed?
• What do you wonder?

I hope they mention the guiding principles, in their own words, of course.