Recently, my colleague Mrs. Shink,  showed me this picture. She was baking macrons with her family. She told me she was going to use it with some of her second graders.  I asked her if I could use it too.

I brought the picture into a second grade class. I gave each student a color copy of it. I asked, what do you notice? What do you wonder? Here is what they said:

I wonder why there is a spot with no circle.

I wonder if someone ate one.

I notice there are 7 on the top row and 8 on the other rows.

I notice they look like cinnamon buns.

I notice some have holes and cracks.

I notice they are different sizes.

I notice that if you go down there are 5 and the one with no spot, there is 4.

I notice there is a metal thing underneath the cookies. I wonder if they just came out of the oven.

I notice there is one small one and the rest are big.

I notice that under the top, there is one, two, three, four, (runs her finger across each row under the top row).  They can be lined up into an 8 row and a 5, I mean 4 (runs her finger down each column). There are 8 going across and 4 going down.  If you take the top (row) away.

At this point, I noticed that some students were thinking about the context of the picture, some were organizing the objects into groups, some were noticing characteristics of the objects. I was particularly interested in the last student who spoke. I wondered if this student was thinking about decomposing the array to make it “easier” to see.

I gave the students more information about the picture.  I told them where it came from.  I also told them that one was missing because Mrs. Shink had eaten one.  Then, I asked them if they could figure out how many macrons were left after Mrs. Shink ate one.

They got right to work.  Many students started counting by ones.  Some students organized the cookies into two groups – ones that were darker and ones that were lighter – and then counted each group and added them together. A few students skip counted by groups or added groups. I noticed some students orally skip counting by fives.  A different student was adding 8s on the side of his paper. I asked the class if they could somehow show me their thinking so that when I took their pictures with me, I would be able to understand how they counted the cookies.  Many students started labeling each cookie with a number: 1, 2, 3, 4, etc.  The students who were orally skip counting wrote an addition equation:  5 + 5 +5 +5 + 5 +5 +5 +4 = 39.   I wondered, “what is the difference between skip counting and using repeated addition?”

When I originally planned this lesson, I was anticipating that the routine would inspire discussion about multiplication.  In my head, I remembered a second grade standard about introducing arrays as representations of multiplication.  I was wrong.

Here is the standard that I was thinking of:

Use addition to find the total number of objects arranged in rectangular arrays with up to 5 rows and up to 5 columns; write an equation to express the total as a sum of equal addends.

What do I notice?

The word multiplication is never mentioned.  The size of the array is limited to 5×5.

As I was reflecting about this lesson, I realized that I was remembering the story wrong. Recently, I watched Graham Fletcher’s shadowcon talk about becoming a better storyteller.  In it, he challenged us to find one standard in the grade level you teach and discover something new about it. Is there something you currently teach that isn’t in the standards? He suggested:

• Find that standard and explore it more deeply.
• Draw it or use tools to support understanding.
• Be dumb. Surround yourself with brilliance.
• Be vulnerable.

This was my chance.  I decided to start by re-reading the Common Core Progression for Operations and Algebraic Thinking.  I have read this document many times and I will read it many more.  I always learn something new. Immediately, this sentence jumped out at me.  “In Equal Groups, the role of the factors differ.  One factor is the number of objects in a group (like any quantity in addition and subtraction situations), and the other is a multiplier that indicates the number of groups.”  We have spent a lot of time in our 3rd grade meetings discussing how three groups of 5 items is different than 5 groups of 3 items, but 3×5=5×3. This is one of the topics we always leave simmering.  Our understanding has gotten richer and more dense over time.

However, I haven’t taken the opportunity to explore this topic with second grade teachers, especially as it relates to addition, as it relates to cookies cooling on a rack.  As I re-read the progressions, I wondered how many students were being given the opportunity to simmer in repeated addition for awhile?  How many second grade teachers had been given the opportunity to deeply explore the relationship between addition and multiplication, and what about subtraction and division?

Recently, I have been watching a few fourth  grade teachers bang their heads against the wall as they try to convince their students that adding 13 forty seven times is not efficient. I have felt helpless. I ask,  “Have you tried showing them arrays with smaller numbers?  Have you tried using the Number Talks Images site?  Have you tried having them compare strategies and articulate someone else’s understanding?”   Yes. Yes. and Yes. Commence banging.

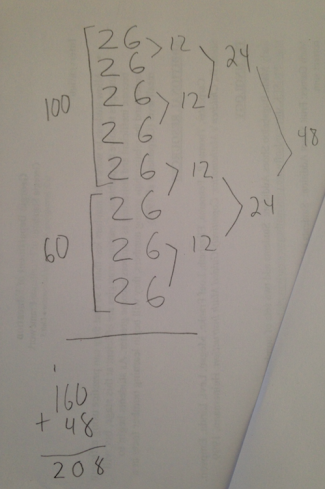
As I write, I am wondering, maybe what we need to do is put these students back on the stove?  We keep trying to pull them towards multiplication, but maybe what they really need is to dive a little deeper into their understanding of repeated addition.  Last week, one student was trying to use an open array to show 26 x 8.  He didn’t want to break the 26 into 20 + 6.  He wanted to use 26+26.  What should I do with this? Graham Fletcher might say, “Draw it. Use tools to understand it.”

Here is my example of what I see these students doing when they are confronted with a two digit by one digit multiplication problem.

We want them to do this:

When we try to convince them to decompose by place value, they push back.  They don’t want to.  They want to use repeated addition.  What if we honored that?  I mean, what if we honored that while simultaneously trying to moving them forward.  What if we let them simmer?  What if we intentionally tried to connect multiplication to repeated addition?

When I sat down to draw in an effort to further my own understanding of how repeated  addition connets to multiplication, here is what I came up with:

Wow!  Graham Fletcher was right. I learned a ton.  I realized that decomposing 26 into 20 +6 might not be helpful to students if they don’t understand the 20 as being equivalent to 2 x 10. I also learned that there are a lot of steps in between using repeated addition and using an open array and the distributive property to solve multiplication problems.

Let me be clear. I am NOT suggesting that we teach students all the steps that I just did. The drawings above represent my journey towards understanding the story better.  My next step is to go back to the fourth grade teachers.  I will retell my story of repeated addition and multiplication.  Then, I will listen carefully and unassumingly to their stories. Together, we will map out the next chapter in the book.

 

 

 

I work as a K-5 math interventionist in two rural Maine schools. Last week I helped to facilitate a staff meeting at one of the two schools I work in. Both schools have implemented Learning Rounds or Instructional Rounds as part of their professional development. This staff meeting was meant to be a time of reflection for this staff as they concluded their first year of learning rounds in their school.

This was quite an accomplishment for both staff and administrators in this building. Learning rounds have not been met with open arms in all of the buildings in our district. In fact this is only the third of four elementary schools to adopt them for math. In order to facilitate the discussion and reflection at this staff meeting, our district math coach and I decided to revisit concerns voiced by this staff at the beginning of the year. We rephrased statements they had placed on a pro/con chart at a September staff meeting into belief statements and gave them back.

Teachers found that many of their concerns were outweighed by the benefits reaped from the learning rounds. Teachers had the opportunity to observe and to be observed at least twice over the course of the year. One of the things that surprised many teachers in this building was that they learned more from observing their peers (even if they were a 5th grade teacher observing a Kindergarten teacher), than they did from being observed.

The focus of our learning rounds are the 8 Mathematical Practices. We had chosen two practices on which to focus at the beginning of the year. This staff had chosen to look at MP#1 Make sense of problems and persevere in solving them, and MP#3 Construct viable arguments and critique the reasoning of others. For each round in which they were observed, teachers worked hard to consider these practices and how the tasks they chose  and planned would provide an opportunity for their students to engage in them. They also participated as observers and had a chance to look for evidence of one of the practices in their colleague’s classrooms using a “Look For” sheet similar to the one below.

This “scavenger hunt” has resulted in a much deeper understanding of the practices for the teachers that have taken part.

Learning rounds have proven to be a powerful tool used to  improve mathematics instruction in our district. As facilitators, we have learned important lessons about how to keep them positive. For instance, setting and reviewing norms such as confidentiality and active listening before each round, providing teachers with PD on the practices we have chosen, and ensuring there is plenty of time to debrief in small observation groups and as a whole staff when possible, are all extremely important.

Personally, my favorite part about them is seeing lightbulbs come on for teachers as they take ownership of their own teaching and learning.  The process requires teachers to take risks in their teaching, and in their learning of new mathematical ideas. Through these risks, we are growing as teachers and learners.