II am a K-12 math coach and I never took Calculus. I hated math in High School. I hated it even more in college. It is really challenging for me to memorize formulas, vocabulary, math facts…. anything really. I am a slow processor, but a fast talker.  I won’t remember anything unless I truly understand it which takes a looooonng time.

When I was a kid, I never knew my multiplication facts. I just couldn’t memorize them. So I taught myself some tricks. Trick #1: count really fast. If I knew 6 x 5 was 30, then I could just count up really fast to figure out 6×7.

You know what I am talking about: 6×5 is 30 so six times 7 must be 31,32,32,34,35,36, 37,38,39,40,41,42. In my head it sounded more like this

“thirtyone thirtytwo th-three,

th-four, five, th-six!” (head bobbing every so slightly- almost imperceptively.)

“th-eight,th-nine, fty, ftyone, forty two!”

Super fast. Right?

Speed matters. Right?

At some point, someone tried to teach me a trick to remember the nines, but it didn’t make sense to me so I never remembered it. Eventually, I figured out that I could use 9×9=81 to figure out 9×8 by subtracting 10 and adding one because that was the same as subtracting 9.  That was as close as I got to using the properties of operations and, at the time, I had no idea that what I was doing had anything to do with the properties of operations. I just thought it was handy that 9 was so close to ten.

Anyway, I didn’t really learn a whole lot of math as a K-12 student. Most of the understanding that I have now has been developed since I started teaching. Now, I love math. I love learning. Now, I know my math facts. I don’t need to use tricks. I don’t even need to use the properties. Using and understanding the associative and distributive properties over time eventually led me to recall multiplication facts. I own them. I can even recall them pretty quickly.  More importantly, now, I have a deep understanding of the properties of operations and the major role they play in our number system.

Every year, I stretch myself to expand my understanding of the properties of operations. I read about them, I ask questions about them, and I play with them A LOT.

This year, I decided it was time I played with Calculus. I thought about taking a Calculus class, but I don’t really want to take a class. I just want to learn; on my own, in a messy, not linear, no-time-crunch, kind of way. I just want to play with Calculus.

I am a little nervous. Sometimes, Calculus seems like a big, burly, sand throwing, dodge-ball-pelting, kind of playmate. Usually this happens when I let myself get into a space where I think I should know something. I get distracted by the little voice in my head that says, “you should know that word.  You should know that symbol.  You should. You should. You should.” Then, it isn’t fun anymore. So, I stop. I walk away. I wait for the curiosity to bubble up again.

The first day of school, my colleague/friend/mentor/math-mate Robyn told me she was trying something a little different with her AP Calculus class this year. She said she was going to give her AP Calc students a problem from Paul Forrester that she adapted. She was hoping her students would struggle a bit and, hopefully, develop an appetite for some important information. She seemed excited about starting the year with a problem. She hoped her students would ask a lot of questions as they solved this problem.  I asked if I could try it. She scribbled the problem on a piece of paper for me.

Suppose a door that is pushed open at time t=0 and slams shut again at time t=7s. While the door is in motion, the number of degrees, d, from the closed position, is modeled by this equation. How fast is the door moving at the instant when t=1s?

One of the first things that I said was, “If  the door was slammed, why did it take seven seconds to close?” She laughed. “Okay,” she said, “maybe it didn’t slam.”

Over the next few days, whenever I had a moment- sitting in the car while my kids were at soccer practice, while I was running, driving around the school district – I would think about the door.  Finally, when I had a minute, I opened Desmos and started a graph.  You can take a look at it here, if you want. Please remember, I am sharing my messy learning with you. I am not looking for feedback, right now. I am happy to answer questions.

Seeing the graph really helped me wrap my head around the problem. I wondered a couple of things:

• Does a negative exponent always signify exponential decay?
• Can I call the curved part of the graph a “parabola” even though it is attached to a decaying exponential curve?  What do we call a function that is part quadratic and part exponential?
• Does the “peak” of the “parabola” represent the moment in time when the door started closing? Is that why 100 degrees shows up twice? Once, when the door reached 100 degrees on the way out and, again, when the door reached 100 degrees on it’s way back to the door jam?
• Can I use the formula for speed to solve this problem?  If speed is measured by distance traveled divided by time spent traveling, can I measure the difference in degrees between two moments in time and divide it by the time it took the door to travel that distance?

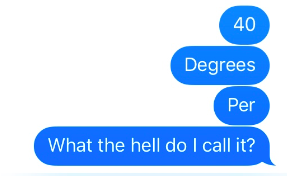
I decided to try this. I think I found the difference in degrees between the door’s location at 0 seconds and 7 seconds and divided it by 7.  I can’t find the scrap of paper that I worked on. I texted Robyn.

She responded:

I decided to call her because I couldn’t explain it in a text.  She asked me to explain what I had found. As I was explaining, I realized that my time span was too long. She reminded me that I was trying to find the speed at 1 second. I was averaging 7 seconds. She re-iterated the word, “instantaneous.”

Instantaneous.

I put the problem aside for the night. The next day, after school, I went back to Desmos.

I added some more points to my table. What if I found the degrees at .99 of a second? That is pretty close to instantaneous, right? This is when the problem solving started to get really fun.

I went back to the drawing board.  I started plugging in points with ridiculous amounts of nines in them. At one point, I went too far. I was using the calculator on my computer. It got tired of my nines. It started rounding.

I walked away again. I went back to work, soccer practice, dinner making, life, but I kept thinking about the door. I couldn’t wait to find those few minutes in my day where I could open my Desmos graph and tinker around some more.

At this point, I found a serindipitous mention on my Twitterfeed. My friend Chase Orton had shared a blog post about the importance of collaboration between HS teachers and elementary teachers.  I shared my thinking with Chase. He asked me to see if I could use a visual approach to the problem.  I thought about that for awhile.

Yesterday, I stopped by Robyn’s office and we chatted about what I had learned so far. We captured our conversation on her whiteboard:

As we were talking, I noticed that self doubt creeped in every time Robyn used a math term to capture what I had described.

I described the change in distance divided by the change in time.

She wrote a “triangle d” symbol on the board.

That little voice started whispering, “You don’t know what that means.”

I described how I was  finding the slopes of really short lines on the graph.

She asked me what we called the line that went through a circle.

I almost panicked, but I didn’t. I was with Robyn. I don’t need to panic with Robyn. Instead, I told her about the voice. I told her I struggled with recall. I told her I wanted to understand but I couldn’t remember what it was called.

She said, “it starts with an “S”.”

I remembered a problem that I was solving with Chase last spring. “Secant?”

“Yup. What about the line that touches a point on the outside of the circle?”

I asked, “What does it start with?

“T”

“Tangent?”

“Yup.” Then, she talked for a little while about how the slopes of the little lines were related to secants and tangents.

I told her what I had noticed about place value patterns when I was solving the door problem. I noticed that I was trying to find the difference between a number super close to 1 and 1.  The delta change (am I using this correctly?) is always going to be 1 whatever the furthest place value to the right is called: one hundredth, one thousandth…..one millionth……one infiniti-th?

Robyn helped me articulate that I was trying to get as close to zero as possible. She introduced a new word.

Limit.

I wondered if I needed a symbol to represent this distance that I can’t really pin down.

Robyn challenged me to try  this:

She also gave me the second problem that her AP Calculus class tried. I am excited to work on both. I will let you know how it goes.